判断下列函数的奇偶性:
(1) ; (2)
; (2)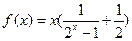 ;
;
(3)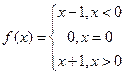 .
.
在平面直角坐标系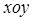 中,直线
中,直线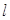 的参数方程为:
的参数方程为: (
(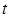 为参数).
为参数).
以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线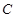 的极坐标方程为:
的极坐标方程为: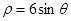 .
.
(1)求曲线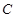 的直角坐标方程;
的直角坐标方程;
(2)若曲线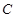 与直线
与直线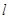 交于
交于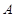 ,
,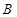 两点,点
两点,点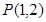 ,求
,求 的最小值.
的最小值.
如图,在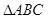 中,
中,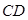 是
是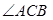 的角平分线,
的角平分线,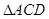 的外接圆交
的外接圆交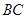 于
于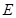 ,
,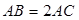 .
.
(1)求证: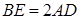 ;
;
(2)若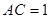 ,
,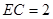 ,求
,求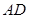 的长.
的长.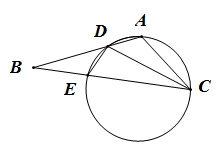
设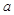 为实数,函数
为实数,函数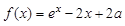 ,
,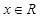 .
.
(1)求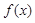 的单调区间与极值;
的单调区间与极值;
(2)求证:当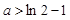 且
且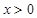 时,
时,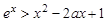 .
.
已知双曲线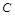 :
: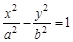
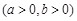 的焦距为
的焦距为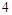 ,以原点为圆心,实半轴长为半径的圆和直线
,以原点为圆心,实半轴长为半径的圆和直线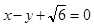 相切.
相切.
(1)求双曲线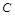 的方程;
的方程;
(2)设点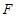 为双曲线
为双曲线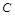 的左焦点,试问在
的左焦点,试问在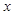 轴上是否存在一定点
轴上是否存在一定点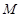 ,过点
,过点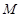 任意作一直线
任意作一直线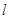 与双曲线
与双曲线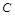 交于
交于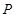 ,
,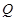 两点,使得
两点,使得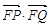 为定值?若存在,求出此定值及点
为定值?若存在,求出此定值及点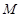 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,在直三棱柱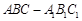 中,
中,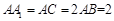 ,且
,且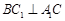 .
.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)设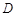 是
是 的中点,判断并证明在线段
的中点,判断并证明在线段 上是否存在点
上是否存在点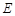 ,使
,使 ‖平面
‖平面 ;若存在,求三棱锥
;若存在,求三棱锥 的体积.
的体积.