设命题p:函数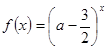 是R上的减函数,
是R上的减函数,
命题q:函数f(x)=x2-4x+3在 上的值域为[-1,3],
上的值域为[-1,3],
若“p且q”为假命题,“p或q”为真命题,求 的取值范围.
的取值范围.
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从A、B、C三个区中抽取6个工厂进行调查.已知A、B、C区中分别有18, 27,9个工厂.
(1)求从A、B、C区中应分别抽取的工厂个数;
(2)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
在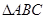 中,角
中,角 、
、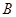 、
、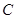 所对的边分别为
所对的边分别为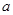 、
、 、
、 .若
.若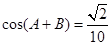 ,
, .
.
(1)求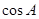 和
和 的值;
的值;
(2)若 ,求
,求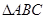 的面积.
的面积.
设函数
(1)当 曲线
曲线 处的切线斜率
处的切线斜率
(2)求函数的单调区间与极值;
(3)已知函数 有三个互不相同的零点0,
有三个互不相同的零点0, ,且
,且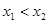 。若对任意的
。若对任意的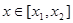 ,
,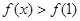 恒成立,求m的取值范围。
恒成立,求m的取值范围。
已知椭圆 的离心率
的离心率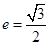 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
(1)求椭圆的方程;
(2)设直线 与椭圆相交于不同的两点
与椭圆相交于不同的两点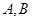 ,已知点
,已知点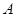 的坐标为(
的坐标为( ),点
),点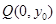 在线段
在线段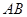 的垂直平分线上,且
的垂直平分线上,且 ,求
,求 的值
的值