已知等差数列 的公差
的公差 大于0,且
大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 ,且
,且

(1)求数列 、
、 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,试比较
,试比较
 的大小,并说明理由
的大小,并说明理由
(本题满分共13分)已知正项数列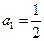 ,函数
,函数 。(1)若正项数列
。(1)若正项数列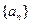 满足
满足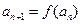 (
(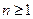 且
且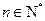 ),试求出
),试求出 由此归纳出通项
由此归纳出通项 ,并证明之;(2)若正项数列
,并证明之;(2)若正项数列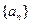 满足
满足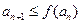 (
(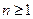 且
且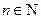 ),数列
),数列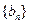 满足
满足 ,其和为
,其和为 ,求证
,求证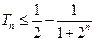 。
。
(本题满分共13分)已知函数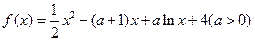 (1)求函数
(1)求函数 的单调递减区间;(2)当
的单调递减区间;(2)当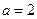 时,函数
时,函数 在
在 有零点,求
有零点,求 的最大值。
的最大值。
为了美化环境,构建两型社会,市城建局打算在广场上建造一个绚丽多彩的矩形花园,中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为2米,如图所示,设矩形花坛的长为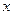 ,宽为
,宽为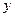 ,整个矩形花园面积为
,整个矩形花园面积为 。(1)试用
。(1)试用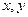 表示S;(2)为了节约用地,当矩形花坛的长为多少米时,新建矩形花园占地最少,占地多少平米?
表示S;(2)为了节约用地,当矩形花坛的长为多少米时,新建矩形花园占地最少,占地多少平米?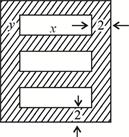
(本题满分共12分)如图,在 中,
中,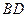 为
为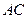 边上高,
边上高,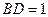 ,
,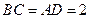 ,沿
,沿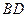 将
将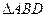 翻折,使得
翻折,使得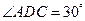 ,得到几何体
,得到几何体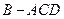 。(1)求证:
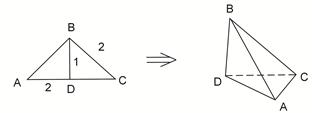
。(1)求证: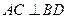 ;
;
(2)求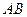 与平面
与平面 成角的正切值。
成角的正切值。
(本题满分共12分)某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100头猪,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100头猪的感染数,得到如下资料:
| 日期 |
4月1日 |
4月2日 |
4月3日 |
4月4日 |
4月5日 |
| 温差 |
10 |
13 |
11 |
12 |
7 |
| 感染数 |
23 |
32 |
24 |
29 |
17 |
(1)求这5天的平均感染数;(2)从4月1日至4月5日中任取2天,记感染数分别为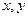 用
用 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中 视为同一事件,并求
视为同一事件,并求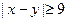 的事件A的概率。
的事件A的概率。