已知a=3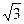 ,c=2,B=150°,求边b的长及S△。
,c=2,B=150°,求边b的长及S△。
抛物线 (p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(1)若线段AB的垂直平分线交x轴于N(x0,0),比较x0与3p大小;
(2)若直线l的斜率依次为p,p2,p3,…,线段AB的垂直平分线与x轴的交点依次为N1,N2,N3,…,求 +
+ +…+
+…+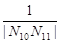 的值.
的值.
已知 的顶点A、B在椭圆
的顶点A、B在椭圆 ,点
,点 在直线
在直线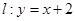 上,且
上,且
(1)当AB边通过坐标原点O时,求 的面积;
的面积;
(2)当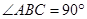 ,且斜边AC的长最大时,
,且斜边AC的长最大时,
求AB所在直线的方程。
如图,A,B,C三个观察哨,A在B的正南,两地相距6km,C在B的北偏东60°,两地相距4km.在某一时刻,A观察哨发现某种信号,并知道该信号的传播速度为1km/s;4秒后B,C两个观察哨同时发现这种信号。在以过A,B两点的直线为y轴,以线段AB的垂直平分线为x轴的平面直角坐标系中,指出发了这种信号的地点P的坐标。
在直角坐标系 中,点P是曲线C上任意一点,点P到两点
中,点P是曲线C上任意一点,点P到两点 ,
, 的距离之和等于4,直线
的距离之和等于4,直线 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若
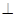
 ,求k的值。
,求k的值。
已知二次函数 (
( 是常数,且
是常数,且 )满足条件:
)满足条件: ,且方程
,且方程 有两个相等实根.
有两个相等实根.
(1)求 的解析式;
的解析式;
(2)是否存在实数 ,使
,使 的定义域和值域分别为
的定义域和值域分别为 和
和 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.