设数列 满足 其中 为实数,
(Ⅰ)求数列
的通项公式
(Ⅱ)设
,求数列
的前
项和
;
(Ⅲ)若
对任意
成立,证明
(本小题满分12分)
如图,已知在坐标平面xOy内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△ PMN的面积为
PMN的面积为 ,点A的坐标为(1+
,点A的坐标为(1+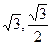 ),
), 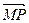 =m·
=m·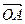 (m为常数),
(m为常数),
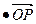


(1)求以M、N为焦点且过点P的椭圆方程;
(2)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分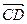 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。
本小题满分12分)
某商店搞促销活动,规则如下:木箱内放有5枚白棋子和5枚黑棋子,顾客从中一次性任意取出5枚棋子,如果取出的5枚棋子中恰有5枚白棋子或4枚白棋子或3枚白棋子,则有奖品,奖励办法如下表:
| 取出的棋子 |
奖品 |
| 5枚白棋子 |
价值50元的商品 |
| 4枚白棋子 |
价值30元的商品 |
| 3枚白棋子 |
价值10元的商品 |
如果取出的不是上述三种情况,则顾客需用50元购买商品.
(1)求获得价值50元的商品的概率;
(2)求获得奖品的概率 ;
;
(3)如果顾客所买商品成本价为10元,假设有 10 000人次参加这项促销活动,则商家可以获得的利润大约是多少?(精确到元)
10 000人次参加这项促销活动,则商家可以获得的利润大约是多少?(精确到元)
(本小题满分12分)
有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计).有人应用数学知识作如下设计:在钢板的四个角处各切去一个小正方形,剩余部分围成一个长方体,该长方体的高是小正方形的边长.
(1)请你求出这种切割、焊接而成的长方体容器的最大容积V1; (2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积V2>V1.
(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积V2>V1.
(本小题满分12分)
已知函数f(x)=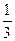 x3+
x3+ ax2+ax-2(a∈R),
ax2+ax-2(a∈R),
(1)若函数f(x)在区间(-∞,+∞)上为单调增函数,求实数a的取值范围;
(2)设A(x1,f(x1))、B(x2,f(x2))是函数f(x)的两个极值点,若直线AB的斜率不小于- ,求实数a的取值范围.
,求实数a的取值范围.
(本小题满分12分)
已知向量a=(1,1),b=(1,0),c满足a·c=0,且|a|=|c|,b·c>0
(1)求向量c;
(2)若映射f:(x,y)→(x′,y′)=xa+yc;
①求映射f下(1,2)的原象;
②若将(x,y)作点的坐标,问是否存在直线 使得直线
使得直线 上任一点在映射f的作用下,仍在直线上,若存在求出的
上任一点在映射f的作用下,仍在直线上,若存在求出的 方程,若不存在说明理由.
方程,若不存在说明理由.