设椭圆
其相应于焦点
的准线方程为
.
(Ⅰ)求椭圆
的方程;
(Ⅱ)已知过点
倾斜角为
的直线交椭圆
于
两点,求证:
;
(Ⅲ)过点
作两条互相垂直的直线分别交椭圆
于
和
,求
的最小值
某单位招聘面试,每次从试题库随机调用一道试题,若调用的是
类型试题,则使用后该试题回库,并增补一道 类试题和一道
类试题和一道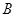 类型试题入库,此次调题工作结束;若调用的是
类型试题,则使用后该试题回库,此次调题工作结束。试题库中现共有
道试题,其中有
道
类型试题和
道
类型试题,以
表示两次调题工作完成后,试题库中
类试题的数量。
类型试题入库,此次调题工作结束;若调用的是
类型试题,则使用后该试题回库,此次调题工作结束。试题库中现共有
道试题,其中有
道
类型试题和
道
类型试题,以
表示两次调题工作完成后,试题库中
类试题的数量。
(Ⅰ)求
的概率;
(Ⅱ)设
,求
的分布列和均值(数学期望)。
设函数
(I)求函数
的最小正周期;
(II)设函数
对任意
,有
,且当
时,
,求函数
在
上的解析式。
函数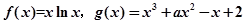
(1)如果函数 单调减区调为
单调减区调为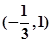 ,求函数
,求函数 解析式;
解析式;
(2)在(1)的条件下,求函数 图象过点
图象过点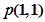 的切线方程;
的切线方程;
(3)若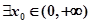 ,使关于
,使关于 的不等式
的不等式 成立,求实数
成立,求实数 取值范围.
取值范围.
已知椭圆 的离心率
的离心率 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点重合,过椭圆右焦点
的焦点重合,过椭圆右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于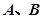 两点.
两点.
(1)求椭圆标准方程;
(2)设点 ,且
,且 ,求直线
,求直线 方程.
方程.
函数
(1) 时,求
时,求 最小值;
最小值;
(2)若 在
在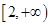 是单调增函数,求
是单调增函数,求 取值范围.
取值范围.