命题"若函数 在其定义域内是减函数,则 "的逆否命题是()
| A. | 若 ,则函数 在其定义域内不是减函数 |
| B. | 若
,则函数
在其定义域内不是减函数 |
| C. | 若 ,则函数 在其定义域内是减函数 |
| D. | 若 ,则函数 在其定义域内是减函数 |
如图,四棱锥 中,底面 为平行四边形, 底面 .
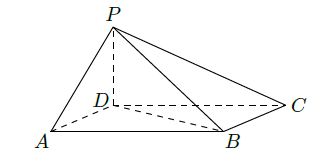
(1)证明: ;
(2)设 ,求棱锥 的高.
已知等比数列
中,
,
(1)
为数列
前
项的和,证明:
.
(2)设
,求数列
的通项公式;
已知平面上的线段
及点
,在
上任取一点
,线段
长度的最小值称为点
到线段
的距离,记作
.
⑴ 求点
到线段
的距离
;
⑵ 设
是长为2的线段,求点集
所表示图形的面积;
⑶ 写出到两条线段
距离相等的点的集合
,其中
,
是下列三组点中的一组.对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
①
.
②
.
③
.
已知数列
和
的通项公式分别为
,
(
),将集合
中的元素从小到大依次排列,构成数列
。
⑴ 求
;
⑵ 求证:在数列
中、但不在数列
中的项恰为
;
⑶ 求数列
的通项公式。
已知
是底面边长为1的正四棱柱,
是
和
的交点.
⑴ 设
与底面
所成的角的大小为
,二面角
的大小为
.求证:
;
⑵ 若点
到平面
的距离为
,求正四棱柱
的高.
