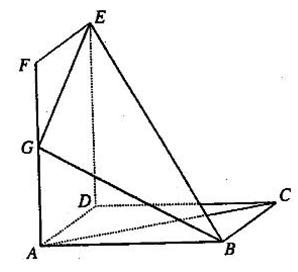
已知不等式x2–3x+t<0的解集为{x|1<x<m, mÎR}
(1)求t, m的值;
(2)若f(x)= –x2+ax+4在(–∞,1)上递增,求不等式log a (–mx2+3x+2–t)<0的解集。
已知函数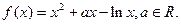
(I)若函数 在
在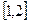 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(II)令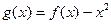 ,是否存在实数
,是否存在实数 ,当
,当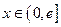 (
( 是自然常数)时,函数
是自然常数)时,函数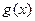
的最小值是3若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(改编)(Ⅲ)当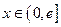 时,证明:
时,证明: .
.
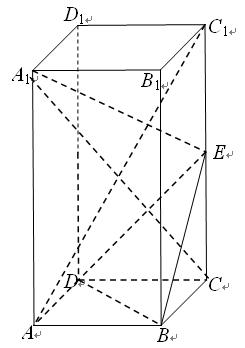
在正四棱柱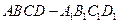 中,
中, ,
, 为
为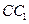 的中点.
的中点.
求证:(I) ∥平面
∥平面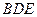 ;(II)
;(II)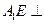 平面
平面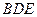 ;
;
(自编)(Ⅲ)若E为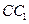 上的动点,试确定
上的动点,试确定 点的位置使直线
点的位置使直线 与平面
与平面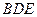 所成角的余弦值是
所成角的余弦值是 .
.
某地高三十校联考数学第I卷中共有8道选择题,每道选择题
有4个选项,其中只有一个是正确的;评分标准规定:“每题只选一项,答对得5分,不答
或答错得0分。”某考生每道题都给出一个答案,已确定有5道题的答案是正确的,而其余
选择题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还
有一道因不了解题意只能乱猜,试求出该考生:
已知向量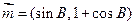 与向量
与向量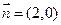 的夹角为
的夹角为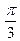 ,
,
在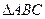 中,
中,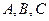 所对的边分别为
所对的边分别为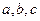 且
且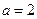 .(改编成)
.(改编成)
(I)求角B的大小;
(Ⅱ)若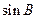 是
是 和
和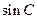 的等比中项,求
的等比中项,求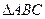 的面积。
的面积。
如图所示,正方形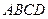 和矩形
和矩形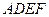 所在平面相互垂直,
所在平面相互垂直,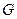 是
是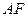 的中点.
的中点.
(I)求证: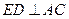 ;
;
(Ⅱ)若直线 与平面
与平面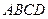 成45o角,求异面直线
成45o角,求异面直线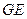 与
与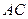 所成角的余弦值.
所成角的余弦值.