已知椭圆 的上顶点为
的上顶点为 ,左右焦点分别为
,左右焦点分别为 ,直线
,直线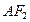 与圆
与圆 :
: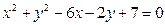 相切,若椭圆上点
相切,若椭圆上点 使得
使得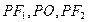 成等比数列
成等比数列
求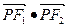
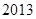 年
年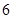 月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为
月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为 、
、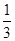 、
、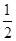 、
、 ,并且各个环节的直播收看互不影响.
,并且各个环节的直播收看互不影响.
(1)现有该班甲、乙、丙三名同学,求这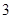 名同学至少有
名同学至少有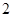 名同学收看发射直播的概率;
名同学收看发射直播的概率;
(2)若用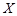 表示该班某一位同学收看的环节数,求
表示该班某一位同学收看的环节数,求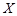 的分布列与期望.
的分布列与期望.
在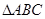 中,
中, 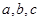 分别是角
分别是角 的对边,且
的对边,且 .
.
(1)求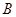 的大小; (2)若
的大小; (2)若 ,
,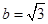 ,求
,求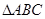 的面积.
的面积.
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为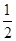 .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
(1)求椭圆C的方程;
(2)设直线l1的斜率k>0,在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形为菱形?如果存在,求出m的取值范围;如果不存在,请说明理由.
已知函数f(x)=ln x-ax(a∈R).
(1)讨论函数f(x)的单调区间;
(2)若函数g(x)=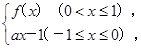 且g(x)≤1恒成立,求实数a的取值范围.
且g(x)≤1恒成立,求实数a的取值范围.
已知数列{an}的前n项和Sn=n2+1,数列{bn}是首项为1,公比为b的等比数列.
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Tn.