已知
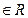 ,
,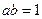 ,
,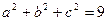 ,求
,求 的最大值
的最大值
已知复数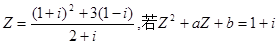 ,
,
求实数a、b 的值.
已知数列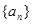 满足
满足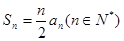 ,
, 是
是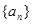 的前
的前 项的和,并且
项的和,并且 .
.
(1)求数列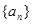 的前
的前 项的和;
项的和;
(2)证明:
已知椭圆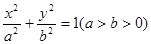 的离心率为
的离心率为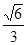 ,长轴长为
,长轴长为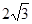 ,直线
,直线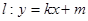 交椭圆于不同的两点A、B.
交椭圆于不同的两点A、B.
(1)求椭圆的方程;
(2)求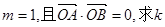 的值(O点为坐标原点);
的值(O点为坐标原点);
(3)若坐标原点O到直线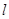 的距离为
的距离为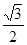 ,求
,求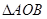 面积的最大值.
面积的最大值.
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
求点A到平面A1DE的距离;
求证:CF∥平面A1DE,
求二面角E-A1D-A的平面角大小的余弦值.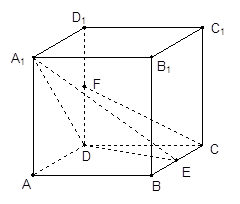
某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人).
(1)共有多少种安排方法?
(2)其中甲、乙两人都被安排的概率是多少?
(3)甲、乙两人中至少有一人被安排的概率是多少?