如图,在四棱锥 中,底面
中,底面 ABCD是正方形,侧棱
ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F。
交PB于点F。
(I)证明 平面
平面 ;
;
(II)证明 平面EFD;
平面EFD;
(III)求二面角 的大小。
的大小。
某省进行高考改革,外语实行等级考试,其他学科分值如下表:
| 科目 |
语文 |
数学 |
科目A |
科目B |
科目C |
科目D |
| 分值 |
180 |
150 |
120 |
100 |
100 |
100 |
有老师建议语文放在首场,数学与科目A不相邻,按这位老师的建议安排考试,前三科总分不小于400的概率为多少?
(2)若前三场科目中要安排语文,求前三场考试总分ξ的分布列及期望值.
如图,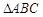 中,
中,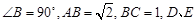 两点分别是线段
两点分别是线段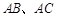 的中点,现将
的中点,现将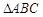 沿
沿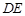 折成直二面角
折成直二面角 。
。
(Ⅰ)求证: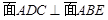 ;(Ⅱ)求直线
;(Ⅱ)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.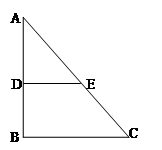

已知各项均为正数的数列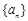 满足:
满足: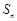 为数列
为数列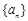 的前
的前 项和,且 2,
项和,且 2,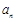 ,
,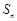 成等差数列.
成等差数列.
(1)求数列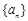 的通项公式;
的通项公式;
(2)若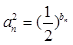 ,
,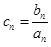 求数列
求数列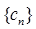 的前
的前 项和.
项和.
在ΔABC中,角A,B,C所对的边分别为a,b,c,已知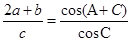

(1)求角C的大小,
(2)若c=2,求使ΔABC面积最大时,a,b的值.
已知函数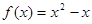 ,
,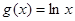 .
.
(Ⅰ)若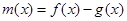 ,
,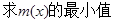 。
。
(Ⅱ)若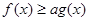 恒成立,求实数
恒成立,求实数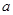 的值;
的值;
(Ⅲ)设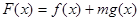
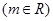 有两个极值点
有两个极值点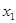 、
、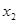 (
(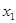
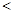
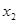 ),求实数
),求实数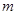 的取值范围,并证明
的取值范围,并证明 .
.