(本小题满分12分)
将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体
(Ⅰ)从这些小正方体中任取1个,求其中至少有两面涂有颜色的概率;
(Ⅱ)从中任取2个小正方体,求2个小正方体涂上颜色的面数之和为4的概率。
(本小题满分13分)
已知 ,函数
,函数 ,记曲线
,记曲线 在点
在点 处切线为
处切线为 与x轴的交点是
与x轴的交点是 ,O为坐标原点。
,O为坐标原点。
(I)证明:
(II)若对于任意的 ,都
,都 有
有 成立,求a的取值范围。
成立,求a的取值范围。
(本小题满分13分)
如图,已知四棱柱ABCD—A1B1C1D1中,A1D⊥底面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2。
(I)求证:C1D//平面ABB1A1;
(II)求直线BD1与平面A1C1D所成角的正弦值;
(Ⅲ)求二面角D—A1C1—A的余弦值。
(本小题满分13分)
一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、5,现从盒子中随机抽取卡片。
(I)若从盒子中有 放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;
放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;
(II)若从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当取到一张记有偶数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望。
(本小题满分13分)
如图,在四边形ABCD中,AB=3,AD=BC=CD=2,A=60°。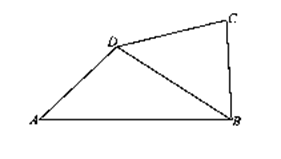
(1)求 的值;
的值;
(2)求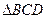 的面积。
的面积。

(本小题满分12分)
如图,在正方体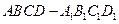 中,
中,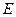 、
、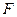 分别是
分别是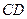 、
、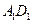 中点
中点
(1)求证: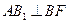 ;
;
(2)求证: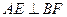 ;
;
(3)棱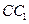 上是否存在点
上是否存在点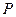 ,使
,使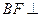 平面
平面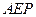 ,若存在,确定点
,若存在,确定点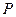 位置;若不存在,说明理由.
位置;若不存在,说明理由.