(本小题满分12分)
如图所示,在正三棱柱 中,底面边长为
中,底面边长为 ,侧棱长为
,侧棱长为 ,
, 是棱
是棱 的中点.
的中点.
|
(Ⅰ)求证: 平面
平面 ;
;
 的大小;
的大小; 到平面
到平面 的距离.
的距离.生产A,B两种元件,其质量按测试指标划分为:指标大于或等于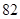 为正品,小于
为正品,小于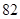 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各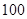 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 |
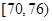 |
 |
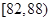 |
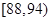 |
 |
| 元件A |
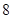 |
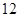 |
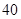 |
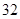 |
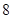 |
| 元件B |
 |
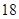 |
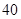 |
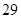 |
 |
(Ⅰ)试分别估计元件A,元件B为正品的概率;
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量 的分布列和数学期望;
的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
在公比为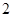 的等比数列
的等比数列 中,
中,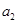 与
与 的等差中项是
的等差中项是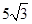 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数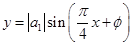 ,
,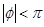 ,的一部分图像如图所示,
,的一部分图像如图所示, ,
, 为图像上的两点,设
为图像上的两点,设 ,其中
,其中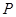 与坐标原点
与坐标原点 重合,
重合,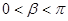 ,求
,求 的值.
的值.
已知数列 ,
, 满足:
满足: .
.
(1)若 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 ,且
,且 .
.
① 记 ,求证:数列
,求证:数列 为等差数列;
为等差数列;
② 若数列 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项 应满足的条件.
应满足的条件.
已知椭圆 过点
过点 ,椭圆
,椭圆 左右焦点分别为
左右焦点分别为 ,上顶点为
,上顶点为 ,
, 为等边三角形.定义椭圆C上的点
为等边三角形.定义椭圆C上的点 的“伴随点”为
的“伴随点”为 .
.
(1)求椭圆C的方程;
(2)求 的最大值;
的最大值;
(3)直线l交椭圆C于A、B两点,若点A、B的“伴随点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.椭圆C的右顶点为D,试探究ΔOAB的面积与ΔODE的面积的大小关系,并证明.
如图1, ,
, 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段 和曲线段
和曲线段 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥 上某点
上某点 分别修建与
分别修建与 ,
, 平行的栈桥
平行的栈桥 、
、 ,且以
,且以 、
、 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段 的方程是
的方程是 ,曲线段
,曲线段 的方程是
的方程是 ,设点
,设点 的坐标为
的坐标为 ,记
,记 .(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
(1)求 的取值范围;
的取值范围;
(2)试写出三角形观光平台 面积
面积 关于
关于 的函数解析式,并求出该面积的最小值
的函数解析式,并求出该面积的最小值