(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
定义变换 :
: 可把平面直角坐标系上的点
可把平面直角坐标系上的点 变换到这一平面上的点
变换到这一平面上的点 .特别地,若曲线
.特别地,若曲线 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线 在变换
在变换 下的不动点.
下的不动点.
(1)若椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程. 并求出当
的标准方程. 并求出当 时,其两个焦点
时,其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标;
(2)当 时,求(1)中的椭圆
时,求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换 :
: (
( ,
, )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.
)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为 ,求
,求 .
.
△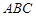 中,角
中,角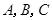 的对边分别为
的对边分别为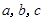 ,且
,且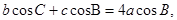
(Ⅰ)求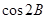 ;
;
(Ⅱ)若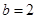 且
且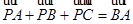 ,求△
,求△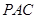 面积最大值.
面积最大值.
设数列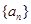 的前n项和为
的前n项和为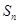 ,满足
,满足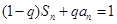 ,且
,且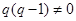 .
.
(Ⅰ)求证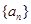 是等比数列;
是等比数列;
(Ⅱ)若存在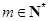 使得
使得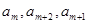 成等差数列,求
成等差数列,求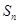 .
.
在平面直角坐标系 中,已知
中,已知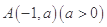 ,
,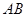 是圆
是圆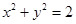 的一条直径,
的一条直径,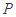 是动点,且直线
是动点,且直线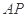 与
与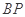 的斜率之积等于
的斜率之积等于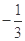 .
.
(1)求动点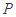 的轨迹方程;
的轨迹方程;
(2)设直线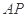 和
和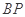 分别与直线
分别与直线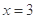 交于点
交于点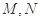 ,问:是否存在点
,问:是否存在点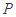 使得
使得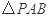 与
与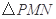 的面积相等?若存在,求出点
的面积相等?若存在,求出点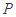 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分14分)已知函数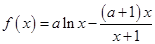 ,其中
,其中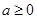 .
.
(Ⅰ)当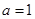 时,求曲线
时,求曲线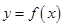 在
在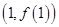 处的切线方程;
处的切线方程;
(Ⅱ)讨论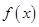 在其定义域上的单调性.
在其定义域上的单调性.