同时抛三枚骰子,求下列事件的概率
(1)第一枚骰了点数大于4,第二枚点数为偶数,第三枚点数为奇数
(2)第一枚骰子点数大于有,第二枚点数为偶数
(3)第三枚点数为偶数
(本小题满分14分)已知{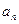 }(
}( 是正整数)是首项是
是正整数)是首项是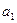 ,公比是
,公比是 的等比数列.
的等比数列.
(1)求和: ;
;
(2)由(1)的结果归纳概括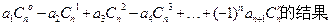
并加以证明;
(3)设 是等比数列的前
是等比数列的前 项的和,求
项的和,求
(本小题满分12分)如图所示,平面 平面
平面 ,
, 是等边三角形,
是等边三角形, 是矩形,
是矩形,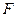 是
是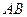 的中点,
的中点, 是
是 的中点,
的中点, 与平面
与平面 成
成 角.
角.
(1)求证: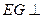 平面
平面 ;
;
(2)若 ,求二面角
,求二面角 的度数;
的度数;
(3)当 的长是多少时,
的长是多少时, 点到平面
点到平面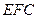 的距离为
的距离为 ?并说明理由
?并说明理由
甲、乙、丙三人组成一组,参加一个闯关游戏团体赛,三人各自独立闯关,其中甲闯关成功的概率为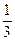 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为 ,每人闯关成功得2分,三人得分之和记为小组团体总分.
,每人闯关成功得2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
(本小题满分12分)如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且二面角A-DC-E为直二面角。
(1)求证:CD⊥DE;(2)求AE与面DEC所成的角.
(本小题满分12分)美国次贷危机引发全球金融动荡,波及中国沪深两大股市,甲、乙、丙3人打算趁股市低迷之际买入股票。三人商定在圈定的10只股票中各自随机购买1只(假定购买时,每只股票的基本情况完全相同)
(1)求甲、乙、丙3人恰好买到相同股票的概率;
(2)求甲、乙、丙3人中至少有2人买到相同股票的概率.