(本小题满分12分)从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组 、第二组
、第二组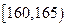 ;…第八组
;…第八组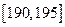 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(I)求第六组、第七组的频率并补充完整频率分布直方图;
(II)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为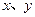 ,求满足
,求满足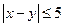 的事件概率;
的事件概率;
(III)从最后三组中任取3名学生参加学校篮球队,用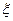 表示从第八组中取到的人数,求
表示从第八组中取到的人数,求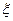 的分布列及其数学期望。
的分布列及其数学期望。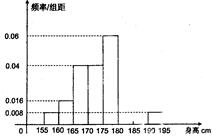
已知函数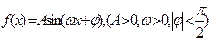 的图象与y轴的交点为(
的图象与y轴的交点为(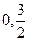 ),它在y轴右侧的第一个最大值点和最小值点分别为
),它在y轴右侧的第一个最大值点和最小值点分别为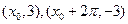 .
.
(1)求函数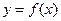 的解析式;
的解析式;
(2)求这个函数的单调递增区间和对称中心.
已知非零向量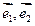 不共线,且
不共线,且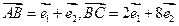 ,
, ,
,
(1)求证:A、B、D三点共线
(2)试确定实数k的值,使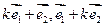 共线
共线

(1)利用“五点法”列表并画出函数 在长度为一个周期的闭区间的简图
在长度为一个周期的闭区间的简图
(2)并说明该函数图象可由y=sinx(x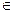 R)的图象经过怎样平移和伸缩变换得到的。
R)的图象经过怎样平移和伸缩变换得到的。
(1)已知向量 ,且A、B、C三点共线,求k的值.
,且A、B、C三点共线,求k的值.
(2)已知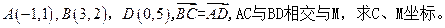
设函数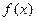 对任意
对任意 ,都有
,都有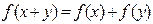 ,
,
且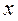 > 0时,
> 0时,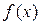 < 0,
< 0, .
.
(1)求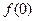 ;
;
(2)求证: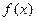 是奇函数;
是奇函数;
(3)请写出一个符合条件的函数;
(4)证明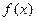 在R上是减函数,并求当
在R上是减函数,并求当 时,
时,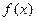 的最大值和最小值
的最大值和最小值