已知函数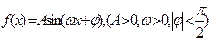 的图象与y轴的交点为(
的图象与y轴的交点为(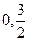 ),它在y轴右侧的第一个最大值点和最小值点分别为
),它在y轴右侧的第一个最大值点和最小值点分别为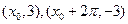 .
.
(1)求函数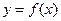 的解析式;
的解析式;
(2)求这个函数的单调递增区间和对称中心.
如图,已知椭圆
与
的中心在坐标原点
,长轴均为
且在
轴上,短轴长分别为
,
,过原点且不与
轴重合的直线
与
的四个交点按纵坐标从大到小依次为
,记
,
和
的面积分别为
和
.
(1)当直线
与
轴重合时,若
,求
的值;
(2)当
变化时,是否存在与坐标轴不重合的直线
,使得
?并说明理由.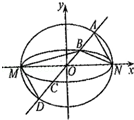
设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.
如图,某地质队自水平地面
三处垂直向地下钻探,自
点向下钻到
处发现矿藏,再继续下钻到
处后下面已无矿,从而得到在A处正下方的矿层厚度为
.同样可得在
处正下方的矿层厚度分别为
,
,且
.过
的中点
且与直线
平行的平面截多面体
所得的截面
为该多面体的一个中截面,其面积记为
中.
(1)证明:中截面
是梯形;
(2)在
中,记
边上的高为
,面积为
.在估测三角形
区域内正下方的矿藏储量(即多面体
的体积
)时,可用近似公式
估=
中
来估算.已知
试判断
估与
的大小关系,并加以证明.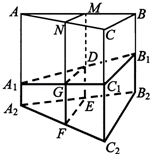
已知
是等比数列
的前
项和,
成等差数列,且
.
(1)求数列
的通项公式;
(2)是否存在正整数
,使得
?若存在,求出符合条件的所有
的集合;若不存在,说明理由.
在
中,角
对应的边分别是
,已知
.
(1)求角
的大小;
(2)若
的面积
,
,求
的值.