(本小题满分12分)
甲,乙两人进行射击比赛,每人射击 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 |
5 |
8 |
7 |
9 |
10 |
6 |
| 乙 |
6 |
7 |
4 |
10 |
9 |
9 |
(Ⅰ)根据上表中的数据,判断甲,乙两人谁发挥较稳定;
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过 的概率.
的概率.
随着国家政策对节能环保型小排量车的调整,两款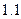 升排量的Q型车、R型车的销量引起市场的关注。已知2010年1月Q型车的销量为
升排量的Q型车、R型车的销量引起市场的关注。已知2010年1月Q型车的销量为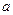 辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式:
辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式: .
.
(1)求Q型车前n个月的销售总量Sn的表达式;
(2)比较两款车前n个月的销售总量Sn与Tn的大小关系;
(3)试问从第几个月开始Q型车的月销售量小于R型车月销售量的20%,并说明理由.
(参考数据
 )
)
已知函数 ,且函数
,且函数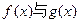 的图象关于直线
的图象关于直线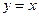 对称,又
对称,又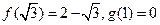 .
.
(1)求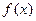 的值域;
的值域;
(2)是否存在实数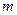 ,使命题
,使命题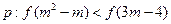 和
和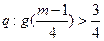 满足复合命题
满足复合命题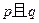 为真命题? 若存在, 求出
为真命题? 若存在, 求出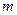 的范围; 若不存在, 说明理由.
的范围; 若不存在, 说明理由.
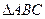 中内角
中内角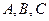 的对边分别为
的对边分别为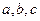 ,
,
向量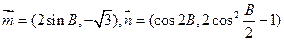 且
且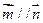
(Ⅰ)求锐角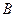 的大小,
的大小,
(Ⅱ)如果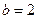 ,求
,求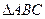 的面积
的面积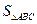 的最大值
的最大值
(本小题满分10分)
已知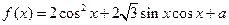 ,
,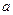 为实常数。
为实常数。
(I)求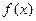 的最小正周期;
的最小正周期;
(II)若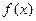 在
在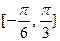 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求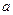 的值。
的值。
(本小题满分10分)
已知数列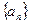 中,
中,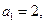 且点P
且点P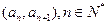 在直线
在直线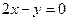 上.
上.
(1)求数列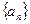 的通项公式;
的通项公式;
(2)设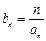 ,求数列
,求数列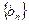 的前
的前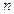 项和
项和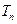 .
.