(本小题满分12分)
如图 ,
, 是圆
是圆 的的直径,点
的的直径,点 是弧
是弧 的中点,
的中点, ,
,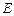 分别是
分别是 ,
,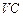 的中点,
的中点,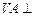
平面 .
.
(Ⅰ)求异面直线 与
与 所成的角;
所成的角;
(Ⅱ)证明  平面
平面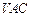 .
.
已知定点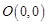 ,
,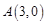 ,动点
,动点 到定点
到定点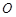 距离与到定点
距离与到定点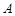 的距离的比值是
的距离的比值是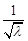 .
.
(Ⅰ)求动点 的轨迹方程,并说明方程表示的曲线;
的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当 时,记动点
时,记动点 的轨迹为曲线
的轨迹为曲线 .
.
①若 是圆
是圆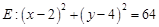 上任意一点,过
上任意一点,过 作曲线
作曲线 的切线,切点是
的切线,切点是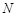 ,求
,求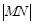 的取值范围;
的取值范围;
②已知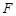 ,
, 是曲线
是曲线 上不同的两点,对于定点
上不同的两点,对于定点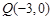 ,有
,有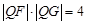 .试问无论
.试问无论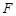 ,
, 两点的位置怎样,直线
两点的位置怎样,直线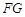 能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
已知数列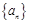 中,
中,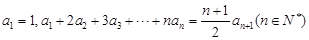
(Ⅰ)求数列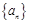 的通项
的通项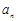 ;
;
(Ⅱ)求数列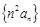 的前
的前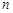 项和
项和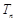 ;
;
(Ⅲ)若存在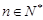 ,使得
,使得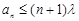 成立,求实数
成立,求实数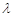 的最小值.
的最小值.
已知定义在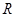 上的函数
上的函数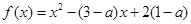 (其中
(其中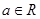 ).
).
(Ⅰ)解关于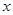 的不等式
的不等式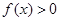 ;
;
(Ⅱ)若不等式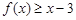 对任意
对任意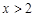 恒成立,求
恒成立,求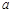 的取值范围.
的取值范围.
在 中,内角
中,内角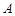 、
、 、
、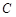 的对边分别为
的对边分别为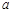 、
、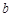 、
、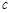 ,已知
,已知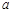 、
、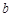 、
、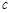 成等比数列,且
成等比数列,且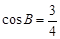 .
.
(Ⅰ)求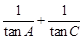 的值;
的值;
(Ⅱ)设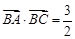 ,求
,求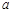 、
、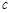 的值.
的值.
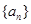 是公比大于
是公比大于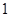 的等比数列,
的等比数列,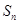 是
是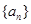 的前
的前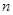 项和.若
项和.若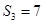 ,且
,且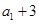 ,
,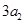 ,
,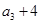 构成等差数列.
构成等差数列.
(Ⅰ)求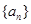 的通项公式.
的通项公式.
(Ⅱ)令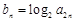 ,求数列
,求数列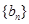 的前
的前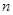 项和
项和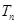 .
.