(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为 、
、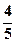 、
、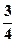 、
、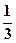 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
(Ⅲ)该选手在选拔过程中回答过的问题个数记为 ,求随机变量
,求随机变量 的分布列和期望.
的分布列和期望.
(本小题满分16分)
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在
40分钟的一节课中,注意力指数p与听课时间t(单位:分钟)之间的关系满足如图
所示的曲线.当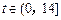 时
时 ,曲线是二次函数图象的一部分,当
,曲线是二次函数图象的一部分,当 时,曲线
时,曲线
是函数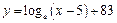 (
(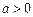 ,
,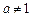 )图象的一部分.根据专家研究,当注意力指数p大于80时学习效果最佳.
)图象的一部分.根据专家研究,当注意力指数p大于80时学习效果最佳.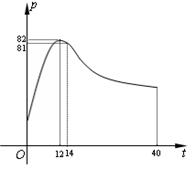
(1)试求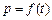 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排核 心内容,能使得学生学习效果最佳?请说明理由.
心内容,能使得学生学习效果最佳?请说明理由.
(本小题满分16分)
已知函数 ,且对于任意
,且对于任意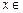 R,恒有
R,恒有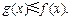
(1)证明: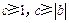 ;
;
(2)设函数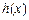 满足:
满足: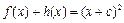 ,证明:函数
,证明:函数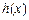 在
在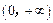 内没有零点.
内没有零点.
(本小题满分14分)
设函数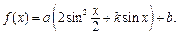
(1)当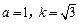 时,求函数
时,求函数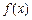 的单调减区间;
的单调减区间;
(2)当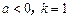 时,函数
时,函数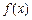 在
在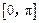 上的值域是[2,3],求a,b的值.
上的值域是[2,3],求a,b的值.
(本小题满分14分)
已知向量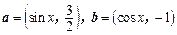 .
.
(1)当a//b时,求 的值;
的值;
(2)设函数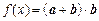 ,问:由函数
,问:由函数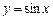 的图象经过怎样的变换可得函数
的图象经过怎样的变换可得函数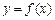 的图象?
的图象?
(本小题满分14分)
设集合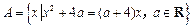 ,
,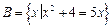 .
.
(1)若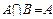 ,求实数
,求实数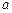 的值;
的值;
(2)求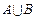 ,
,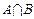 .
.