(本小题满分14分)
如图,在直角梯形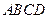 中,
中, ,
,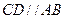 ,
,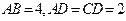 .将
.将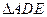 沿
沿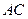 折起,使平面
折起,使平面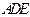
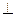 平面
平面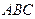 ,得到几何体
,得到几何体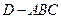 ,如图2所示.
,如图2所示.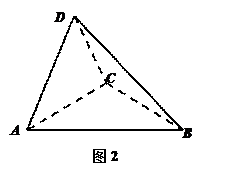 (Ⅰ) 求证:
(Ⅰ) 求证: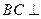 平面
平面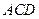 ;
;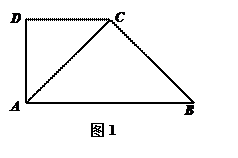 (Ⅱ) 求几何体
(Ⅱ) 求几何体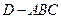 的体积.
的体积.
设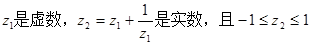
(1)求 | z1| 的值以及z1的实部的取值范围;
(2)若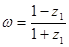 ,求证:
,求证: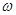 为纯虚数.
为纯虚数.
设复数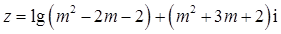 .
.
(Ⅰ)若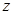 是纯虚数,求实数m的值;
是纯虚数,求实数m的值;
(Ⅱ)若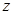 是实数,求实数m的值;
是实数,求实数m的值;
(Ⅲ)若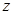 对应的点位于复平面的第二象限,求实数m的取值范围.
对应的点位于复平面的第二象限,求实数m的取值范围.
新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分).
设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.
某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.
(1)根据以上数据建立一个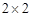 的列联表;
的列联表;
(2)认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?(参考数值: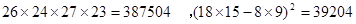 )
)
已知复数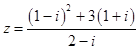 ,若
,若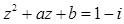 ,
,
(1)求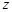 ;
;
(2)求实数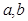 的值.
的值.