(本小题满分14分)
如图,四棱锥 中,
中,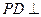 平面
平面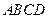 ,底面
,底面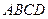 为矩形,
为矩形, ,
,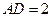 ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ) 边上是否存在一点
边上是否存在一点 ,使得
,使得 平面
平面 ,若存在,求出
,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.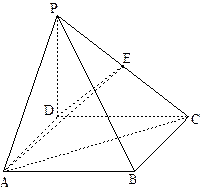
已知椭圆 的焦距为2,点
的焦距为2,点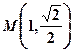 在椭圆
在椭圆 上,
上, 求椭圆
求椭圆 的标准方程;
的标准方程; 若过点
若过点 的直线与
的直线与 中的椭圆交于不同的两点
中的椭圆交于不同的两点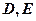 (
( 在
在 、
、 之间);
之间);
试求 与
与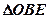 面积之比的取值范围.
面积之比的取值范围.
下图是一几何体的直观图、正(主)视图、侧(左)视图、俯视图
(1)若 为
为 的中点,求证
的中点,求证 :
: 平面
平面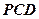 ;
;
(2)求平面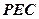 与平面
与平面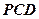 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
从装有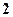 个红球,
个红球,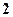 个白球和
个白球和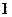 个黑球的袋中逐一取球,已知
个黑球的袋中逐一取球,已知 每个球被抽取的可能性相同.
每个球被抽取的可能性相同.
(1)若抽取后又放回,抽取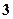 次,分别求恰有
次,分别求恰有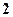 次是红球的概率及抽全三种颜色球的概率;
次是红球的概率及抽全三种颜色球的概率;
(2)若抽取后不放回,求抽完红球所需次数不少于4次的概率;
(3)记红球、白球、黑球对应的号码为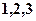 ,现从盒中有放回地先后抽出的两球的号码分别记
,现从盒中有放回地先后抽出的两球的号码分别记
为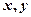 ,记
,记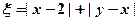 ,求随机变量
,求随机变量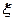 的分布列.
的分布列.
在一个特定的时间段内,以点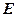 为中心的
为中心的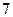 海里以内的海域被设为警戒水域,点
海里以内的海域被设为警戒水域,点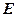 正北55海里处有一雷达观测站
正北55海里处有一雷达观测站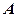 ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点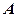 北偏东
北偏东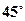 且与点
且与点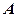 相距
相距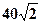 海里的位置
海里的位置 ,经过40分钟又测得该船已经驶到点
,经过40分钟又测得该船已经驶到点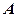 北偏东
北偏东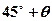 (其中
(其中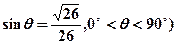 且与点
且与点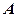 相距
相距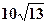 海里的
海里的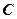 处.
处. 求该船的行驶速度;
求该船的行驶速度; 若该船不改变航行
若该船不改变航行 方向继续行驶,判断它是否会进入警戒线水域,并说明理由.
方向继续行驶,判断它是否会进入警戒线水域,并说明理由.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.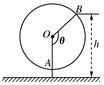
(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?