我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径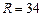 百公里)的中心
百公里)的中心 为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)
为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点) 到火星表面的距离为
到火星表面的距离为 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点) 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点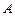 第一次逆时针运行到与轨道中心
第一次逆时针运行到与轨道中心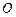 的距离为
的距离为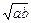 百公里时进行变轨,其中
百公里时进行变轨,其中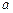 、
、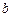 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
底面边长为 的正三棱锥
的正三棱锥 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图. 求
,如图. 求 的各边长及此三棱锥的体积
的各边长及此三棱锥的体积 .
.
如图,四棱锥 中,
中, 为矩形,平面
为矩形,平面 平面
平面 .
.
(1)求证:
(2)若 问
问 为何值时,四棱锥
为何值时,四棱锥 的体积最大?并求此时平面
的体积最大?并求此时平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
如图,在棱长为2的正方体 中,
中, 分别是棱
分别是棱 的中点,点
的中点,点 分别在棱
分别在棱 ,
, 上移动,且
上移动,且 .
.
(1)当 时,证明:直线
时,证明:直线
 平面
平面 ;
;
(2)
是否存在 ,使平面
,使平面 与面
与面 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,四边形 为正方形,
为正方形, 平面
平面 ,
, ,
, 于点
于点 ,
, ,交
,交 于点
于点 .
.
(1)证明:
(2)求二面角 的余弦值。
的余弦值。
如图,正方形 的边长为2,
的边长为2, 分别为
分别为 的中点,在五棱锥
的中点,在五棱锥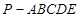 中,
中, 为棱
为棱 的中点,平面
的中点,平面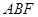 与棱
与棱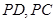 分别交于点
分别交于点 .
.
(1)求证: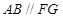 ;
;
(2)若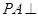 底面
底面 ,且
,且 ,求直线
,求直线 与平面
与平面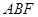 所成角的大小,并求线段
所成角的大小,并求线段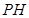 的长.
的长.