(本小题满分12分)
已知函数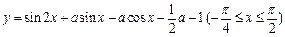 的最大值为2,求实数a的值.
的最大值为2,求实数a的值.
已知函数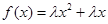 ,
, ,
,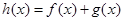 ,其中
,其中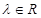 ,且
,且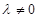 .
.
⑴当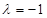 时,求函数
时,求函数 的最大值;
的最大值;
⑵求函数 的单调区间;
的单调区间;
⑶设函数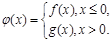 若对任意给定的非零实数
若对任意给定的非零实数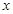 ,存在非零实数
,存在非零实数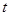 (
( ),使得
),使得 成立,求实数
成立,求实数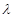 的取值范围.
的取值范围.
已知函数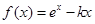 .
.
(Ⅰ)若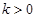 ,且对于任意
,且对于任意 恒成立,试确定实数
恒成立,试确定实数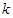 的取值范围;
的取值范围;
(Ⅱ)设函数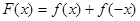 ,
,
求证:
数列{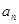 }的前n项和为
}的前n项和为 ,
, .
.
(Ⅰ)设 ,证明:数列
,证明:数列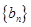 是等比数列;
是等比数列;
(Ⅱ)求数列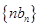 的前
的前 项和
项和 ;
;
(Ⅲ)若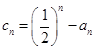 ,
,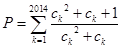 .求不超过
.求不超过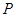 的最大整数的值.
的最大整数的值.
如图所示,圆柱的高为2,底面半径为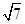 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过 作圆柱的截面交下底面于
作圆柱的截面交下底面于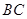 ,四边形ABCD是正方形.
,四边形ABCD是正方形.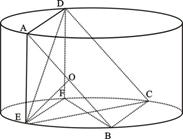
(Ⅰ)求证 ;
;
(Ⅱ)求四棱锥E-ABCD的体积.
某学校餐厅新推出A,B,C,D四款套餐,某一天四款套餐销售情况的条形图如下. 为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
| 满意 |
一般 |
不满意 |
|
| A套餐 |
50% |
25% |
25% |
| B套餐 |
80% |
0 |
20% |
| C套餐 |
50% |
50% |
0 |
| D套餐 |
40% |
20% |
40% |
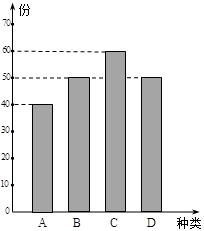
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.