对函数  ,若存在
,若存在 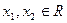 且
且 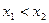 ,使得
,使得  (其中 A, B为常数),则称
(其中 A, B为常数),则称  为"可分解函数"。
为"可分解函数"。
(1)试判断 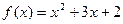 是否为"可分解函数",若是,求出 A, B的值;若不是,说明理由;
是否为"可分解函数",若是,求出 A, B的值;若不是,说明理由;
(2)用反证法证明:  不是"可分解函数";
不是"可分解函数";
(3)若  是"可分解函数",则求 a的取值范围,并写出 A, B关于 a的相应的表达式。
是"可分解函数",则求 a的取值范围,并写出 A, B关于 a的相应的表达式。
设数列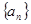 满足
满足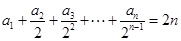 ,
, .
.
(1)求数列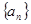 的通项公式;
的通项公式;
(2)设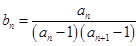 ,求数列
,求数列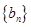 的前
的前 项和
项和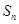 .
.
如图,在三棱锥 中,
中,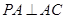 ,
,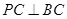 ,
, 为
为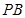 的中点,
的中点, 为
为 的中点,且
的中点,且 为正三角形.
为正三角形.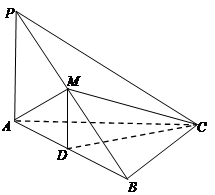
(1)求证: 平面
平面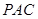 ;
;
(2)若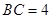 ,
,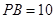 ,求点
,求点 到平面
到平面 的距离.
的距离.
某单位 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在 岁至
岁至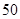 岁
岁
之间.按年龄分组:第1组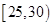 ,第
,第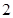 组
组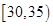 ,第3组
,第3组 ,第
,第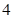 组
组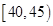 ,第
,第 组
组 ,得到的频率分布直方图如图所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图所示.下表是年龄的频率分布表.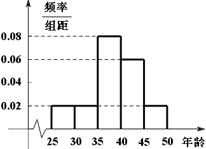
| 区间 |
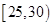 |
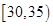 |
 |
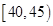 |
 |
| 人数 |
 |
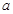 |
 |
(1)求正整数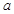 、
、 、
、 的值;
的值;
(2)现要从年龄较小的第 、
、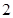 、
、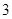 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 人,则年龄在第
人,则年龄在第 、
、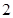 、
、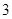 组的人数分别
组的人数分别
是多少?
(3)在(2)的条件下,从这 人中随机抽取
人中随机抽取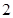 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有 人在第
人在第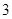 组的概率.
组的概率.
在△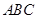 中,角
中,角 、
、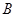 、
、 所对的边分别为
所对的边分别为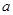 、
、 、
、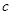 ,且
,且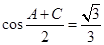 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求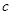 的值.
的值.
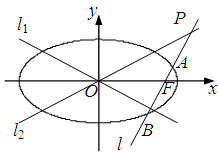
如图,已知椭圆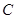 的方程为
的方程为 ,双曲线
,双曲线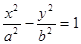 的两条渐近线为
的两条渐近线为 、
、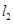 .过椭圆
.过椭圆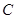 的右焦点
的右焦点 作直线
作直线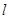 ,使
,使 ,又
,又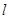 与
与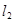 交于点
交于点 ,设
,设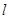 与椭圆
与椭圆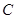 的两个交点由上至下依次为
的两个交点由上至下依次为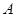 、
、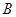 .
.
(1)若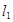 与
与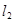 的夹角为
的夹角为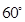 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆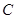 的方程;
的方程;
(2)求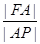 的最大值.
的最大值.