(满分12分)正方体ABCD-A1B1C1D1 的棱长为 2,且AC 与BD 交于点O,E 为棱DD1 中点,以A 为原点,建立空间直角坐标系A-xyz,如图所示.
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点  F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
(Ⅲ)求二面角B1-EA-C 的正弦值.
(本小题满分12分)已知:定义在R上的函数 ,对于任意实数a, b都满足
,对于任意实数a, b都满足 ,且
,且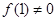 ,当
,当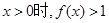 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)证明 在
在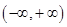 上是增函数;
上是增函数;
(Ⅲ)求不等式 的解集.
的解集.
(本小题满分12分)已知函数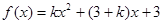 ,其中
,其中 为常数,且
为常数,且
(1)若 ,求函数
,求函数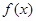 的表达式;
的表达式;
(2)在(1)的条件下,设函数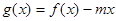 ,若
,若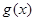 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数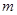 的取值范围;
的取值范围;
(3)是否存在实数 使得函数
使得函数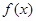 在
在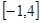 上的最大值是4?若存在,求出
上的最大值是4?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(满分12分)已知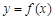 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当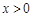 时,
时, .
.
(Ⅰ)求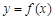 的解析式;
的解析式;
(Ⅱ)问是否存在这样的正数a, b使得当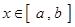 时,函数
时,函数 的值域为
的值域为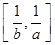 ,若存在,求出所有a, b的值,若不存在,说明理由.
,若存在,求出所有a, b的值,若不存在,说明理由.
(本小题满分12分)已知函数 f(x)=4x2-4ax+(a2-2a+2).
(1)若a=1, 求f(x)在闭区间[0,2]上的值域;
(2)若f(x)在闭区间[0,2]上有最小值3,求实数a的值.
(本小题满分12分 )已知定义在区间(﹣1,1)上的函数 是奇函数,且
是奇函数,且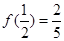 ,
,
(1)确定 的解析式;
的解析式;
(2)判断 的单调性并用定义证明;
的单调性并用定义证明;