(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—1:几何证明选讲
如图,已知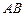 是
是 的直径,
的直径, ,
,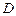 是
是 上两点,
上两点, 于
于 ,
,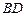 交
交 于
于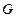 ,交
,交 于
于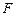 ,
, .
.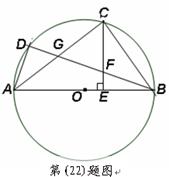
(Ⅰ)求证: 是
是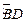 的中点;
的中点;
(Ⅱ)求证: .
.
(本小题满分10分)
已知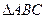 的三个内角A、B、C所对的三边分别是a、b、c,平面向量
的三个内角A、B、C所对的三边分别是a、b、c,平面向量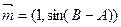 ,平面向量
,平面向量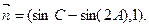
(I)如果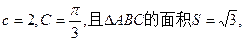 求a的值;
求a的值;
(II)若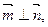 请判断
请判断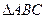 的形状.
的形状.
已知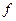 (
(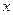 )=
)=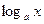 ,
,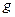 (
(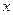 )=
)= 且
且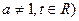 .
.
(Ⅰ)当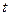 =4,
=4,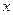 ∈(0,+
∈(0,+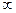 ),且F(
),且F(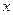 )=
)=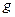 (
(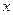 )-
)-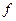 (
(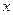 )有最小值2时,求
)有最小值2时,求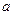 的值;
的值;
(Ⅱ)当0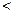
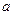
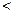 1,
1,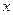 ∈(0,+
∈(0,+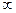 )时,有
)时,有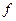 (
(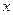 )≥
)≥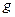 (
(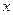 )恒成立,求实数
)恒成立,求实数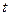 的取值范围.
的取值范围.
经过调查发现,某种新产品在投放市场的100天中,前40天,其价格直线上升,(价格是关于时间的一次函数),而后60天,其价格则呈直线下降趋势,现抽取其中4天的价格如下表所示:
| 时间 |
第4天 |
第32天 |
第60天 |
第90天 |
| 价格(千元) |
23 |
30 |
22 |
7 |
(Ⅰ)写出价格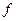 (
(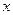 )关于时间
)关于时间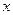 的函数表达式(
的函数表达式(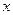 表示投入市场的第
表示投入市场的第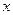 天);
天);
(Ⅱ)若销售量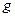 (
(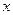 )与时间
)与时间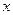 的函数关系是
的函数关系是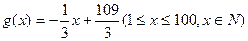 ,求日销售额的最大值,并求第几天销售额最高?
,求日销售额的最大值,并求第几天销售额最高?
已知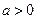 ,函数
,函数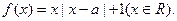
(Ⅰ)当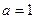 时,求所有使
时,求所有使 成立的
成立的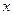 的值;
的值;
(Ⅱ)当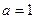 时,求函数
时,求函数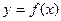 在闭区间
在闭区间 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)试讨论函数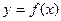 的图象与直线
的图象与直线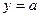 的交点个数
的交点个数
角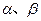 (
(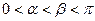 )的终边与单位圆分别交于A、B两点,已知A、B的横坐标分别为
)的终边与单位圆分别交于A、B两点,已知A、B的横坐标分别为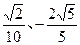 .试求:
.试求:
(Ⅰ)tan(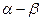 );
);
(Ⅱ)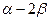 .
.