甲、乙两个箱子中装有大小相同的小球,甲箱中有2个红球和2个黑球,乙箱中装有2个黑球和3个红球,现从甲箱和乙箱中各取一个小球并且交换.
(Ⅰ)求交换后甲箱中刚好有两个黑球的概率;
(Ⅱ)设交换后甲箱中黑球的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
某市居民1999~2003年货币收入 与购买商品支出
与购买商品支出 的统计资料如下表所示:单位:亿元
的统计资料如下表所示:单位:亿元
| 年份 |
1999 |
2000 |
2001 |
2002 |
2003 |
货币收入 |
40 |
42 |
44 |
47 |
50 |
购买商品支出 |
33 |
34 |
36 |
39 |
41 |
(Ⅰ)画出散点图,判断x与Y是否具有相关关系;
(Ⅱ)已知 ,请写出Y对x的回归直线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
,请写出Y对x的回归直线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
调查某桑场采桑员和辅助工桑毛虫皮炎发病情况结果如下表:利用2×2列联表的独立性检验估计“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系会犯错误的概率是多少?
| 采桑 |
不采桑 |
合计 |
|
| 患者人数 |
18 |
12 |
|
| 健康人数 |
5 |
78 |
|
| 合计 |
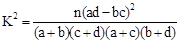
| P(K2≥k) |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
(本小题满分10分)
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
(本小题满分12分)
已知函数
(1)判断函数 的奇偶性;
的奇偶性;
(2)若 在区间
在区间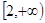 是增函数,求实数
是增函数,求实数 的取值范围。
的取值范围。
(本小题满分12分)
设函数 。
。
(1)当a=1时,求 的单调区间。
的单调区间。
(2)若 在
在 上的最大值为
上的最大值为 ,求a的值。
,求a的值。