(12分)某电视台综艺频道主办一种有奖过关游戏，该游戏设有两关，只有过了第一关，才能玩第二关，每关最多玩两次，连续两次失败者被淘汰出局．过关者可获奖金,只过第一关获奖金900元，两关全过获奖金3600元．某同学有幸参与了上述游戏，且该同学每一次过关的概率均为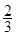
，各次过关与否互不影响．在游戏过程中，该同学不放弃所有机会．
（1）求该同学仅获得900元奖金的概率；
（2）若该同学已顺利通过第一关，求他获得3600元奖金的概率.
（本小题满分13分）若数列
满足
N*）．
（1）求的通项公式;
（2）等差数列
的各项均为正数，其前n项和为
，且
，又
成等比数列，求．
已知函数
.
（Ⅰ）若
在
处取得极大值，求实数a的值；
（Ⅱ）若
，直线
都不是曲线
的切线，求
的取值范围；
（Ⅲ）若
，求在区间［0，1］上的最大值.
已知椭圆
的右焦点为
，实轴的长为
．
（1）求椭圆的标准方程；
（2）过点
作两条互相垂直的直线分别交椭圆于点
和
，求
的最小值．
设数列
的前
项和为
，点
在直线
上，
.
（1）求证：数列是等比数列，并求其通项公式；
（2）设直线
与函数
的图像交于点
，与函数
的图像交于点
，记
（其中
为坐标原点），求数列
的前项和
.
如图，三棱柱ABC﹣A1B1C1的底面是边长为3的正三角形，侧棱AA1垂直于底面ABC，AA1=
，D是CB延长线上一点，且BD=BC．
（1）求证：直线BC1∥平面AB1D；
（2）求三棱锥C1﹣ABB1的体积．