如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
(I) 证明:BD⊥AA1;
证明:BD⊥AA1;
(II)求二面角D—A1A—C的平面角的余弦值;
(III)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(本小题满分14分)已知数列 的前
的前 项和为
项和为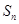 ,且满足
,且满足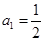 ,
, (
(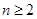 且
且 ).
).
(1)求证:数列 是等差数列;
是等差数列;
(2)求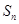 和
和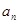 .
.
(本小题满分14分)如图,菱形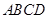 的边长为
的边长为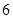 ,
, ,
,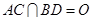 .将菱形
.将菱形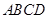 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥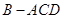 ,点
,点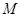 是棱
是棱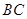 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分12分)移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元. 国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率. 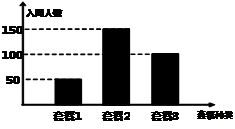
(1)求某人获得优惠金额不低于300元的概率;
(2)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选出两人,求这两人获得相等优惠金额的概率.
(本小题满分12分)设向量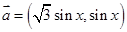 ,
, ,
,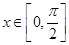 .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数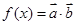 ,求
,求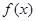 的最大值.
的最大值.
(本小题满分14分)已知函数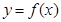 ,
, ,设曲线
,设曲线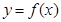 在点
在点 处的切线方程为
处的切线方程为 .如果对任意的
.如果对任意的 ,均有:
,均有:
①当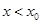 时,
时,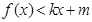 ;
;
②当 时,
时,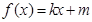 ;
;
③当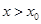 时,
时,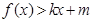 ,
,
则称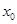 为函数
为函数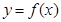 的一个“ʃ-点”.
的一个“ʃ-点”.
(1)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
① ; ②
; ② .(只需写出结论)
.(只需写出结论)
(2)设函数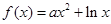 .
.
(ⅰ)若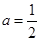 ,证明:
,证明: 是函数
是函数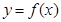 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数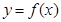 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出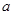 的取值范围.
的取值范围.