已知函数 的导函数
的导函数 的图象上的一个最高点和与它相邻的一个最低点的坐标分别为
的图象上的一个最高点和与它相邻的一个最低点的坐标分别为 ,
, .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位得到函数
个单位得到函数 图象,直线
图象,直线 (
( )与
)与 ,
, 的图象分别交于
的图象分别交于 两点,求
两点,求 的最大值.
的最大值.
如图所示,在矩形ABCD中,AB=3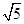 ,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=
,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=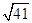 .
.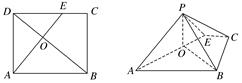
(1)求证:PO⊥平面ABCE;
(2)求二面角EAPB的余弦值.
如图(1),四边形ABCD中,E是BC的中点,DB=2,DC=1,BC=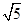 ,AB=AD=
,AB=AD=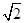 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).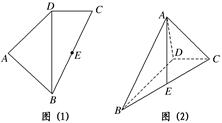
(1)求证:AE⊥平面BDC;
(2)求直线AC与平面ABD所成角的余弦值.
如图,在三棱柱ABCA1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.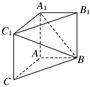
(1)求证:AA1⊥平面ABC;
(2)求二面角A1BC1B1的余弦值;
(3)证明:在线段BC1上存在点D,使得AD⊥A1B,并求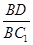 的值.
的值.
如图所示,在多面体ABCD-A1B1C1D1中,上、下两个底面A1B1C1D1和ABCD互相平行,且都是正方形,DD1⊥底面ABCD,AB∥A1B1,AB=2A1B1=2DD1=2a.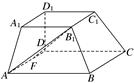
(1)求异面直线AB1与DD1所成角的余弦值;
(2)已知F是AD的中点,求证:FB1⊥平面BCC1B1.
已知函数f(x)=
(1)若x<a时,f(x)<1恒成立,求a的取值范围;
(2)若a≥-4时,函数f(x)在实数集R上有最小值,求实数a的取值范围.