(本小题满分12分)
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示.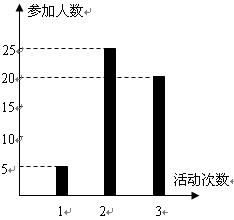
(Ⅰ)求该班学生参加活动的人均次数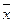 ;
;
(Ⅱ)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率;
(Ⅲ)从该班中任选两名学生,用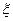 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量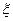 的分布列及数学期望
的分布列及数学期望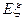 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)
(本小题满分13分)
设命题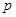 :对任意实数
:对任意实数 ,不等式
,不等式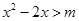 恒成立;命题
恒成立;命题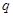 :方程
:方程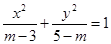 表示焦点在
表示焦点在 轴上的双曲线.
轴上的双曲线.
(I)若命题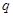 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(II)若命题“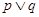 ”为真命题,且“
”为真命题,且“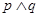 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分13分)
已知抛物线 的顶点在原点,焦点为
的顶点在原点,焦点为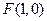 ,且过点
,且过点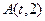 .
.
(1)求t的值;
(2)若直线 与抛物线
与抛物线 只有一个公共点,求实数
只有一个公共点,求实数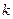 的值.
的值.
(本题满分13分)
把一颗骰子投掷两次,记第一次出现的点数为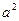 ,第二次出现的点数为
,第二次出现的点数为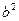 (其中
(其中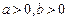 ).
).
(Ⅰ)若记事件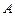 “焦点在
“焦点在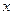 轴上的椭圆的方程为
轴上的椭圆的方程为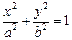 ”,求事件
”,求事件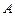 的概率;
的概率;
(Ⅱ)若记事件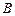 “离心率为2的双曲线的方程为
“离心率为2的双曲线的方程为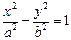 ”,求事件
”,求事件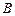 的概率.
的概率.
(本题满分13分)
为了了解某校高中部学生的体能情况,体育组决定抽样三个年级部分学生进行跳绳测试,并将所得的数据整理后画出频率分布直方图.已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.
(I) 求第四小组的频率和参加这次测试的学生人数;
(II) 在这次测试中,学生跳绳次数的中位数落在第几小组内?
(III) 参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
(本小题14分)
|
椭圆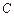 :
: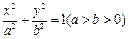 的离心率为
的离心率为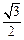 ,且过
,且过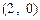 点.
点.
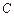 的方程;
的方程;
 :
: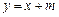 与椭圆
与椭圆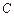 相交时,求m的取值范围;
相交时,求m的取值范围;
 :
: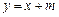 与椭圆
与椭圆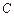 交于
交于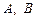 两点,
两点,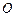 为坐标原点,若
为坐标原点,若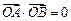 ,求
,求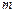 的值。
的值。