（本题14分）为了让更多的人参与2010年在上海举办的“世博会”，上海某旅游公司面向国内外发行一定数量的旅游优惠卡，其中向境外人士发行的是世博金卡（简称金卡），向境内人士发行的是世博银卡（简称银卡）．现有一个由36名游客组成的旅游团到上海参观旅游，其中27名境外游客，其余是境内游客．在境外游客中有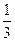
持金卡，在境内游客中有
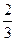持银卡．．
（Ⅰ）在该团中随机采访3名游客，求恰有1人持金卡，至多1人持银卡的概率；
（Ⅱ）在该团的境内游客中随机采访3名游客，设其中持银卡人数为随机变量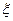
，求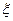的分布列及数学期望
．
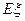已知函数f(x)=(x+a)(bx+2a)是偶函数 (其中a，b是常数)，且它的值域为 
，
（Ⅰ）求f(x)的解析式
将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，将得到的点数分别记为
.
（Ⅰ）求直线
与圆
有公共点的概率；
（Ⅱ）求方程组
只有正数解的概率。
已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），x∈R的最大值是1，其图象经过点
（Ⅰ）求f（x）的解析式；
（Ⅱ）
2011年3月5日某校组织同学听取了温家宝总理所作的政府工作报告，并进行了检测，从参加检测的高一学生中随机抽出60名学生，将其成绩(均为整数)分成六段［40,50),［50,60),…,［90,100］后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：
（Ⅰ）求分数在［70,80)内的频率，并补全这个频率分布直方图；
（Ⅱ）请根据频率分布直方图估计本次考试中的成绩的平均分及中位数（可保留一位小数）.
下面是利用UNTIL循环设计的计算
的一个算法程序．
S＝1
I=1
DO
S=S*I
①
LOOP UNTIL ②
PRINT S
END
（Ⅰ）请将其补充完整；
（Ⅱ）绘制出该算法的流程图．