已知抛物线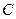 的顶点为坐标原点,椭圆
的顶点为坐标原点,椭圆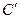 的对称轴是坐标轴,抛物线
的对称轴是坐标轴,抛物线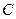 在
在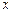 轴上的焦点恰好是椭圆
轴上的焦点恰好是椭圆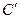 的焦点
的焦点
(Ⅰ)若抛物线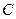 和椭圆
和椭圆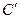 都经过点
都经过点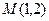 ,求抛物线
,求抛物线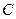 和椭圆
和椭圆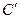 的方程;
的方程;
(Ⅱ)已知动直线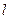 过点
过点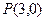 ,交抛物线
,交抛物线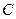 于
于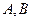 两点,直线
两点,直线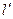 :
: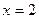 被以
被以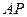 为直径的圆截得的弦长为定值,求抛物线
为直径的圆截得的弦长为定值,求抛物线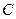 的方程;
的方程;
(Ⅲ)在(Ⅱ)的条件下,分 别过
别过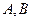 的抛物线
的抛物线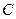 的两条切线的交点
的两条切线的交点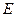 的轨迹为
的轨迹为 ,直线
,直线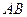 与轨迹
与轨迹 交于点
交于点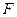 ,求
,求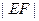 的最小值。
的最小值。
设函数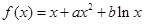 ,其对应的图像为曲线C;若曲线C过
,其对应的图像为曲线C;若曲线C过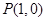 ,且在
,且在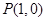 点处的切斜线率
点处的切斜线率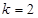
(1)求函数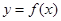 的解析式
的解析式
(2)证明不等式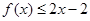 .
.
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲: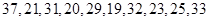
乙: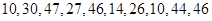
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为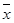 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的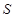 大小为多少?并说明
大小为多少?并说明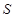 的统计学意义.
的统计学意义.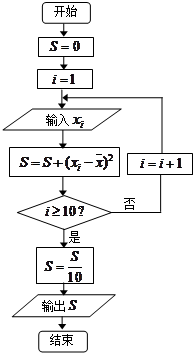
已知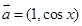 ,
,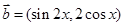 ,且
,且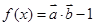
(1)求函数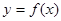
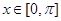 的单调增区间;
的单调增区间;
(2)三角形ABC中,边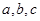 分别为角
分别为角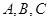 的对边,若
的对边,若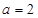 ,B=
,B=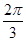 ,且
,且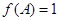 , 求三角形ABC的边
, 求三角形ABC的边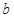 的值.
的值.
已知集合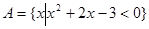 ,
,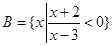 .
.
(1)在区间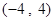 上任取一个实数
上任取一个实数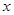 ,求“
,求“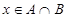 ”的概率;
”的概率;
(2)设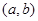 为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中
为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中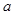 是从集合
是从集合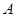 中任取的一个整数,
中任取的一个整数,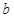 是从集合
是从集合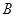 中任取的一个整数,求“
中任取的一个整数,求“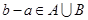 ”的概率
”的概率
已知
(1)求 的值;
的值;
(2)若 是第三象限的角,化简三角式
是第三象限的角,化简三角式 ,并求值.
,并求值.