已知数列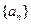 中,
中,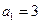 ,
,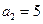 ,其前
,其前 项和
项和 满足
满足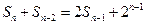
 ,令
,令 .
.
(Ⅰ)求数列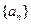 的通项公式;
的通项公式;
(Ⅱ)令 ,求证:
,求证:
① 对于任意正整数 ,都有
,都有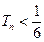 ;
;
② 对于任意的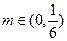 ,均存在
,均存在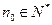 ,使得
,使得 时,
时,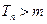 .
.
观察下面表格:
(1)完成表中的频率分布表;
(2)根据表格,画出频率分布直方图;
(3)估计数据落在[10.95,11.35)范围内的概率约为多少?
| 分组 |
频数 |
频率 |
| [10.75,10.85) |
3 |
|
| [10.85,10.95) |
9 |
|
| [10.95,11.05) |
13 |
|
| [11.05,11.15) |
16 |
|
| [11.15,11.25) |
26 |
|
| [11.25,11.35) |
20 |
|
| [11.35,11.45) |
7 |
|
| [11.45,11.55) |
4 |
|
| [11.55,11.65) |
2 |
|
| 合计 |
100 |
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x |
2 |
3 |
4 |
5 |
6 |
| 维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知y对x呈线性相关关系;
试求:(1)线性回归方程y=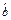 x+
x+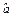 的回归系数
的回归系数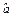 ,
,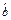 ;
;
(2)估计使用年限为10年时,维修费用是多少?
在一次飞机航程中调查男女乘客的晕机情况,其二维条形图如图:
(1)写出2×2列联表;
(2)判断晕机与性别是否有关?
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| 积极参加班级工作 |
不太主动参加班级工作 |
合计 |
|
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性一般 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?