某次有奖竞猜活动设有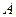
、
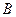两组相互独立的问题，答对问题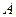可赢得奖金3000元，答对问题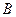可赢得奖金6000元．规定答题顺序可任选，但只有一个问题答对后才能解答下一个问题，否则中止答题，假设你答对问题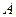、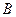的概率依次为
．
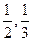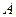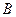（Ⅰ）若你按先后的次序答题，写出你获得奖金的数额
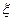的分布列及期望
；
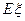（Ⅱ）你认为获得奖金期望的大小与答题顺序有关吗？证明你的结论．
(本题满分14分) 已知正四棱锥P－ABCD中，底面是边长为2的正方形，高为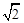
．M为线段PC的中点．
(Ⅰ) 求证：PA∥平面MDB；
(Ⅱ) N为AP的中点，求CN与平面MBD所成角的正切值．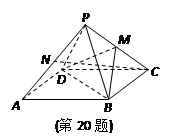
(本题满分14分) 设等差数列{an}的首项a1为a，公差d＝2，前n项和为Sn．
(Ⅰ) 若S1，S2，S4成等比数列，求数列{an}的通项公式；
(Ⅱ) 证明：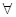
n∈N*, Sn，Sn＋1，Sn＋2不构成等比数列．
(本题满分14分) 设向量α＝(
sin 2x，sin x＋cos x)，β＝(1，sin x－cos x)，其中x∈R，函数f (x)＝α
β．(Ⅰ) 求f (x) 的最小正周期；(Ⅱ) 若f (θ)＝
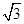，其中0＜θ＜
，求cos(θ＋
)的值．
(本题满分14分) 设函数f (x)＝ln x＋
在(0，
) 内有极值．
(Ⅰ) 求实数a的取值范围；
(Ⅱ) 若x1∈(0，1)，x2∈(1，＋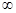
)．求证：f (x2)－f (x1)＞e＋2－．
注：e是自然对数的底数．
(本题满分15分) 如图，椭圆C: x2＋3y2＝3b2(b＞0).
(Ⅰ) 求椭圆C的离心率；
(Ⅱ) 若b＝1，A，B是椭圆C上两点，且 | AB | ＝
，
求△AOB面积的最大值.