设各项均为正数的数列
的前
项和为
,已知
,数列
是公差为
的等差数列.
①求数列
的通项公式(用
表示)
②设
为实数,对满足
且
的任意正整数
,不等式
都成立。求证:
的最大值为
一边长为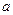 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒.
的小正方形,然后做成一个无盖方盒.
(1)将方盒的容积表示成 的函数
的函数 ;
;
(2)当 是多少时,方盒的容积最大?最大容积是多少?
是多少时,方盒的容积最大?最大容积是多少?
如图:在棱长为1的正方体 —
—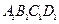 中.
中.
点M是棱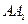 的中点,点
的中点,点 是
是 的中点.
的中点.
(1)求证: 垂直于平面
垂直于平面 ;
;
(2)求平面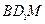 与平面
与平面 所成二面角的平面角(锐角)
所成二面角的平面角(锐角)
的余弦值.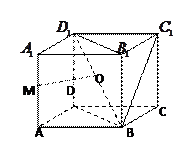
设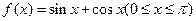
(1)求 的最大值及
的最大值及 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)若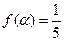 ,求
,求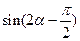 的值.
的值.
从5名男生和4名女生选出4人去参加辩论比赛.
(1)求选出的4人中有1名女生的概率;
(2)设X为选出的4人中的女生人数,求X的分布列及数学期望.
(本小题满分14分)
已知数列
(1)计算x2,x3,x4的值;
(2)试比较xn与2的大小关系;
(3)设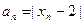 ,Sn为数列{an}前n项和,求证:当
,Sn为数列{an}前n项和,求证:当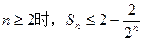 .
.