为了考察冰川的融化状况,一支科考队在某冰川上相距8 的 两点各建一个考察基地.视冰川面为平面形,以过 两点的直线为 轴,线段 的的垂直平分线为 轴建立平面直角坐标系在直线 的右侧,考察范围为到点 的距离不超过 区域;在直线 的左侧,考察范围为到 两点的距离之和不超过 区域.

(Ⅰ)求考察区域边界曲线的方程;
(Ⅱ)如图所示,设线段
是冰川的部分边界线(不考虑其他边界线),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2
,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间.
已知曲线C上的动点P( )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
(1)求曲线C的方程。
(2)过点M(1,2)的直线 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。
已知命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线。命题
轴上的双曲线。命题 曲线
曲线 与
与 轴交于不同的两点,若
轴交于不同的两点,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。
已知函数f(x)=- x3+
x3+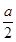 x2-2x(a∈R).
x2-2x(a∈R).
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f′(x)<2(a-1)成立,求实数a的取值范围;
(3)若过点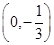 可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
如图,E是以AB为直径的半圆上异于点A、B的点,矩形ABCD所在的平面垂直于该半圆所在的平面,且AB=2AD=2
(1)求证: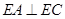
(2)设平面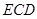 与半圆弧的另一个交点为
与半圆弧的另一个交点为
①试证: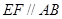
②若 求三棱锥
求三棱锥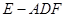 的体积
的体积
已知命题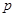 :方程
:方程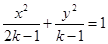 表示椭圆;
表示椭圆; :方程
:方程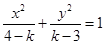 表示双曲线. 若“
表示双曲线. 若“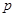 或
或 ”为真,“
”为真,“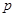 且
且 ” 为假,求实数
” 为假,求实数 的取值范围.
的取值范围.