设
使定义在区间
上的函数，其导函数为
.如果存在实数
和函数
，其中对任意的
都有>0，使得
，则称函数具有性质
.
(1)设函数
，其中
为实数
①求证：函数具有性质
②求函数的单调区间
(2)已知函数
具有性质
，给定
，
，且
，若|
|<|
|,求
的取值范围
已知角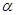
的终边与单位圆交于点
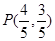（Ⅰ）求出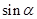
、
、
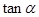的值；（Ⅱ）求
的值．
已知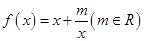
.
(1)若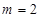
，求函数
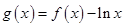在区间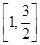
上的最大值；
(2)若函数
在区间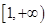
上是减函数，求实数
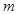的取值范围
某种产品的广告费支出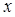
(百万元)与销售额
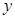(百万元)之间有如下对应数据:
|
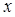2 |
4 |
5 |
6 |
8 |
 |
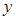30 |
40 |
50 |
60 |
70 |
如果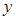与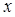之间具有线性相关关系.
(1)作出这些数据的散点图；
(2)求这些数据的线性回归方程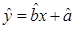
;
(3)预测当广告费支出为9百万元时的销售额。
（参考公式：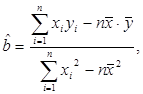
）
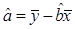、某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成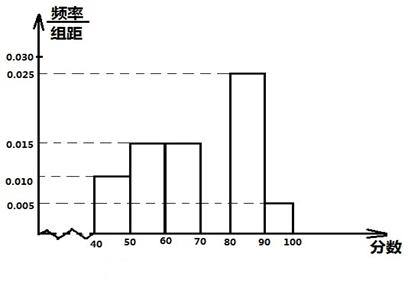
六段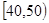
，
…
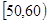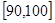后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
（1）求第四小组的频率，并补全这个频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；
、已知
是函数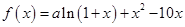
的一个极值点．
(1)求
；(2)求函数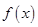
的单调区间．