【2015高考广东，理19】设
，函数
．
（1）求
的单调区间 ；
（2）证明：在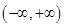
上仅有一个零点；
（3）若曲线
在点
处的切线与
轴平行，且在点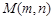
处的切线与直线
平行（
是坐标原点），证明：
．
已知长方形ABCD, AB=2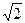
,BC=1.以AB的中点
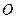为原点建立如图8所示的平面直角坐标系
.
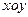(Ⅰ)求以A、B为焦点，且过C、D两点的椭圆的标准方程;
(Ⅱ)过点P(0,2)的直线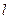
交(Ⅰ)中椭圆于M,N两点,是否存在直线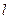,使得以弦MN为直径的圆恰好过原点?若存在,求出直线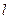的方程;若不存在,说明理由.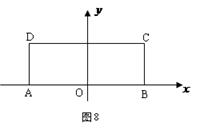
已知A、B分别是椭圆
的左右两个焦点，O为坐标原点，点P
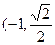）在椭圆上，线段PB与y轴的交点M为线段PB的中点。
（1）求椭圆的标准方程；
（2）点C是椭圆上异于长轴端点的任意一点，对于△ABC，求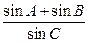
的值。
已知椭圆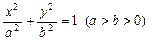
与过点A(2，0)，B(0，1)的直线l有且只有一个公共点T，且椭圆的离心率
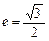．求椭圆方程
如图，在Rt△ABC中，∠CAB=90°，AB=2，AC=
。一曲线E过点C，动点P在曲线E上运动，且保持|PA|+|PB|的值不变，直线l经过A与曲线E交于M、N两点。
（1）建立适当的坐标系，求曲线E的方程；
（2）设直线l的斜率为k，若∠MBN为钝角，求k的取值范围。
已知椭圆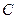
的中心为坐标原点
,一个长轴端点为
,短轴端点和焦点所组成的四边形为正方形，直线
与y轴交于点P（0，m），与椭圆C交于相异两点A、B，且
．
（1）求椭圆方程；
（2）求m的取值范围．