设函数 。
。
(1)若函数 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数 的取值范围;
的取值范围;
(2)求函数 的极值点。
的极值点。
(本小题满分12分)已知 ,
, ,
, 分别为
分别为 三内角
三内角 ,
, ,
, 的对边,
的对边, ,
, ,
,  .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的面积.
的面积.
(本小题满分14分)已知函数 (a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为-1.
(a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为-1.
(Ⅰ)求a的值及函数f(x)的单调区间;
(Ⅱ)证明:当 时,
时, ;
;
(Ⅲ)证明:当 时,
时, .
.
(本小题满分14分)已知椭圆C: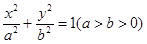 的焦距为4,其长轴长和短轴长之比为
的焦距为4,其长轴长和短轴长之比为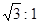 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设F为椭圆C的右焦点,T为直线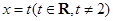 上纵坐标不为0的任意一点,过F作TF的垂线交椭圆C于点P,Q.
上纵坐标不为0的任意一点,过F作TF的垂线交椭圆C于点P,Q.
(ⅰ)若OT平分线段PQ(其中O为坐标原点),求 的值;
的值;
(ⅱ)在(ⅰ)的条件下,当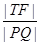 最小时,求点T的坐标.
最小时,求点T的坐标.
(本小题满分12分)对某交通要道以往的日车流量(单位:万辆)进行统计,得到如下记录:
| 日车流量x |
 |
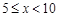 |
 |
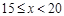 |
 |
 |
| 频率 |
0.05 |
0.25 |
0.35 |
0.25 |
0.10 |
0 |
将日车流量落入各组的频率视为概率,并假设每天的车流量相互独立.
(Ⅰ)求在未来连续3天里,有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率;
(Ⅱ)用X表示在未来3天时间里日车流量不低于10万辆的天数,求X的分布列和数学期望.
(本小题满分12分)如图,在棱长为2的正方体 中,点E,F分别是棱AB,BC上的动点,且AE=BF.
中,点E,F分别是棱AB,BC上的动点,且AE=BF.
(Ⅰ)求证:A1F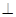 C1E;
C1E;
(Ⅱ)当三棱锥 的体积取得最大值时,求二面角
的体积取得最大值时,求二面角 的正切值.
的正切值.