已知函数
其中
,且
.
(Ⅰ)讨论函数
的单调性;
(Ⅱ)设函数
(
是自然数的底数)。是否存在
,使
在
上为减函数?若存在,求
的取值范围;若不存在,请说明理由。
(本小题满分12分)已知函数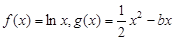 (
(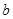 为常数)。
为常数)。
(Ⅰ)函数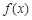 的图象在点(
的图象在点(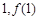 )处的切线与函数
)处的切线与函数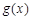 的图象相切,求实数
的图象相切,求实数 的值;
的值;
(Ⅱ)设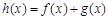 ,若函数
,若函数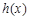 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数 的取值范围;
的取值范围;
(Ⅲ)若 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数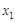 ,
,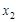 ,都有
,都有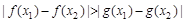 成立,求
成立,求 的取值范围。
的取值范围。
(本小题满分12分)双曲线C与椭圆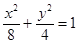 有相同的焦点,直线y=
有相同的焦点,直线y=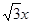 为
为 的一条渐近线.
的一条渐近线.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)过点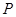 (0,4)的直线
(0,4)的直线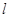 ,交双曲线
,交双曲线 于A,B两点,交x轴于
于A,B两点,交x轴于 点(
点( 点与
点与 的顶点不重合)。当
的顶点不重合)。当 =
=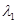
 ,且
,且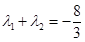 时,求
时,求 点的坐标
点的坐标
(本小题满分12分)设等比数列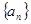 的公比为
的公比为 ,前n项和
,前n项和 。
。
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设 ,记
,记 的前n项和为
的前n项和为 ,试比较
,试比较 与
与 的大小。
的大小。
(本小题满分12分)右图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为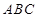 已知
已知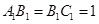 ,
, ,
, ,
, ,
,

(Ⅰ)设点 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(Ⅱ)求二面角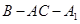 的大小;
的大小;
(本小题满分12分)袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)计分介于20分到40分之间的概率