(本小题满分10分)
等比数列 中,已知
中,已知
(I)求数列 的通项公式;(Ⅱ)若
的通项公式;(Ⅱ)若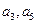 分别为等差数列
分别为等差数列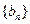 的第3项和第5项,试求数列
的第3项和第5项,试求数列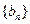 的通项公式及前
的通项公式及前 项和
项和
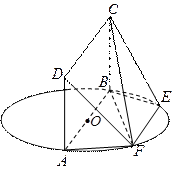
如图, 为圆
为圆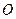 的直径,点
的直径,点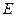 、
、 在圆
在圆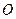 上,
上, ,矩形
,矩形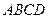 和圆
和圆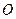 所在的平面互相垂直.已知
所在的平面互相垂直.已知 ,
, .
.
(1)求证:直线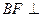 平面
平面 ;
;
(2)求直线 与平面
与平面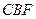 所成角的大小;
所成角的大小;
(3)当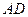 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为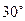 ?
?
已知△ABC三边所在直线方程为 ,
, ,
, ,
, 为坐标原点。
为坐标原点。
(1)求 边上的高所在的直线方程;
边上的高所在的直线方程;
(2)若直线 经过点
经过点 ,且交
,且交 轴负半轴于点
轴负半轴于点 ,交
,交 轴正半轴于点
轴正半轴于点 ,
, 的面积为
的面积为 ,求
,求 的最小值并求此时直线
的最小值并求此时直线 的方程
的方程
如图,在三棱锥 中,
中, ⊥底面
⊥底面 ,
, .
.
(1)求证: ⊥
⊥ ;
;
(2)若 ,求二面角
,求二面角 的大小.
的大小.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
(1)求这个奖杯的体积;
(2)求这个奖杯底座的侧面积.