设
,
是
的反函数.
(Ⅰ)设关于
的方程求
在区间
上有实数解,求
的取值范围;
(Ⅱ)当
(e为自然对数的底数)时,证明:
;
(Ⅲ)当
时,试比较
与4的大小,并说明理由.
设数列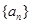 的前
的前 项和为
项和为 已知
已知

(I)设 ,证明数列
,证明数列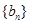 是等比数列;
是等比数列;
(II)求数列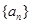 的通项公式.
的通项公式.
. (本小题满分10分)
设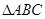 的内角A、B、C所对的边分别为
的内角A、B、C所对的边分别为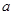 、b、c,已知
、b、c,已知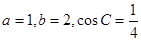
(Ⅰ)求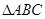 的周长;
的周长;
(Ⅱ)求 的值.
的值.
(1)设x、y、z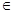 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥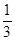 ;
;
(2)设二次函数f (x)=ax2+bx+c(a>0),方程f (x)-x=0有两个实根x1,x2,
且满足:0<x1<x2<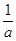 ,若x
,若x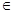 (0,x1)。
(0,x1)。
求证:x<f (x)<x1
已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16。
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:an=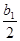 +
+ +
+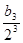 +……+
+……+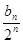 ,(n
,(n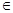 N+),
N+),
求数列{bn}的前n项和Sn。
直线l的方程为(a+1)x+y+2-a=0(a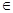 R)。
R)。
(1)若l在两坐标轴上的截距相等,求a的值;
(2)若l不经过第二象限,求实数a的取值范围。