如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD//BC且AD﹥BC,∠DAB=∠ABC=90°,PA= ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。
(1)求二面角M—AD—C的大小;(6分)
(2)如果∠AMD=90°,求线段AD的长。
袋中有同样的球 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机且不返回地摸球,每次摸
个黄色,现从中随机且不返回地摸球,每次摸 个,当两种颜色的球都被摸到时,即停止摸球,记随机变量
个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:.
为此时已摸球的次数,求:.
(1)随机变量 的概率分布; (9分)
的概率分布; (9分)
(2)随机变量 的数学期望与方差.
的数学期望与方差.
(10分)已知: .
.
(1)求: 的取值范围;(5分)
的取值范围;(5分)
(2)求:函数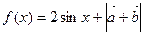 的最小值. (5分)
的最小值. (5分)
(本小题满分14分)
设二次函数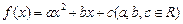 满足下列条件:
满足下列条件:
①当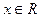 时,其最小值为0,且
时,其最小值为0,且 成立;
成立;
②当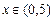 时,
时,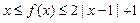 恒成立.
恒成立.
(1)求 的值;
的值;
(2)求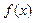 的解析式;
的解析式;
(3)求最大的实数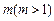 ,使得存在
,使得存在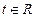 ,只要当
,只要当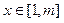 时,就有
时,就有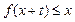 成立
成立
(本小题满分13分)已知:函数 对一切实数
对一切实数 都有
都有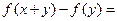
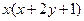 成立,且
成立,且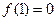 .
.
(1)求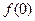 的值;
的值;
(2)求 的解析式;
的解析式;
(3)已知 ,设P:当
,设P:当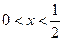 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为 ,求
,求 ∩
∩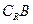 (
( 为全集)
为全集)