(本题12分)口袋里放了12个大小完全一样的小球,其中3个是红色的,
4个是白色的,5个是蓝色的,现从袋中任意取出4个小球,求:
(1) 取出的小球的颜色至少是两种的概率;
(2) 取出的小球的颜色是三种的概率.
探究函数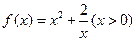 的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
| x |
… |
0.25 |
0.5 |
0.75 |
1 |
1.1 |
1.2 |
1.5 |
2 |
3 |
5 |
… |
| y |
… |
8.063 |
4.25 |
3.229 |
3 |
3.028 |
3.081 |
3.583 |
5 |
9.667 |
25.4 |
… |
已知:函数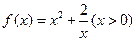 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:
(1)函数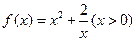 在区间上递增.当
在区间上递增.当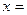 时,
时, ;
;
(2)函数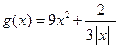 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
已知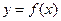 是定义在R上的偶函数,当
是定义在R上的偶函数,当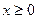 时,
时,
(1)求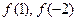 的值;
的值;
⑵求 的解析式并画出简图;
的解析式并画出简图;
⑶讨论方程 的根的情况。(只需写出结果,不要解答过程).
的根的情况。(只需写出结果,不要解答过程).
已知 ,
, 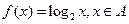
(1)设集合 ,请用列举法表示集合B;
,请用列举法表示集合B;
(2)求 和
和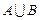 .
.
已知抛物线C的顶点在原点,焦点在y轴正半轴上,点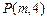 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图, 过抛物线C的焦点的直线从左到右依次与
过抛物线C的焦点的直线从左到右依次与 抛物线C及圆
抛物线C及圆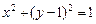 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明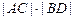 为定值;
为定值;
(Ⅲ)过A、B分别作抛物C的切线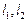 且
且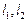 交于点M,求
交于点M,求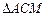 与
与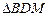 面积之和的最小值.
面积之和的最小值.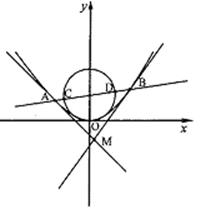
(本小题满分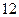 分)
分)
已知函数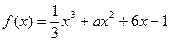 .当
.当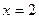 时,函数
时,函数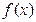 取得极值.
取得极值.
(I)求实数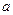 的值;
的值;
(II)若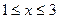 时,方程
时,方程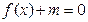 有两个根,求实数
有两个根,求实数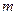 的取值范围.
的取值范围.