如图,四棱锥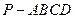 中,侧面
中,侧面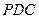 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是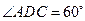 的菱形,
的菱形,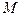 为
为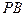 的中点.
的中点.
(Ⅰ) 求证: 平面
平面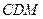 ;
;
(Ⅱ) 求二面角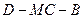 的余弦值.
的余弦值.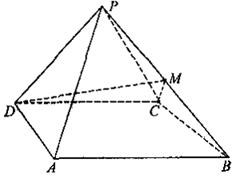
已知四棱锥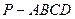 (如图)底面是边长为2的正方形.侧棱
(如图)底面是边长为2的正方形.侧棱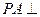 底面
底面 ,
, 、
、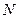 分别为
分别为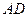 、
、 的中点,
的中点, 于
于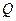 。
。
(Ⅰ)求证:平面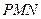 ⊥平面
⊥平面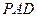 ;
;
(Ⅱ)直线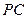 与平面
与平面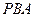 所成角的正弦值为
所成角的正弦值为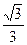 ,求PA的长;
,求PA的长;
(Ⅲ)在条件(Ⅱ)下,求二面角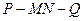 的余弦值。
的余弦值。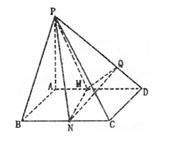
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面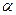 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在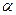 的上方,分别以△
的上方,分别以△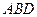 与△
与△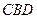 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(Ⅰ)求证:PQ⊥BD;
(Ⅱ)求二面角P-BD-Q的余弦值;
(Ⅲ)求点P到平面QBD的距离.
已知正方体ABCD— 中,E为棱CC
中,E为棱CC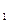 上的动点,
上的动点,
(1)求证: ⊥
⊥ ;
;
(2)当E恰为棱CC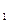 的中点时,求证:平面
的中点时,求证:平面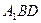 ⊥
⊥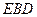 ;
;
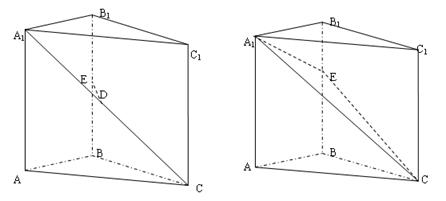
如图直棱柱ABC-A1B1C1中AB=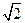 ,AC=3,BC=
,AC=3,BC=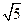 ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。
(1)当E是BB1的中点时,证明:DE//平面A1B1C1;
(2)求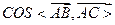 的值
的值
(3)在棱 BB1上是否存在点E,使二面角E-A1C-C是直二面角?若存在求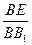 的值,不存在则说明理由。
的值,不存在则说明理由。