已知函数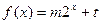 的图象经过点
的图象经过点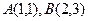 及
及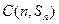 ,
,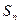 为数列
为数列
的前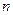 项和.
项和.
(1)求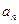 及
及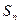 ;
;
(2)若数列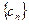 满足
满足 求数列
求数列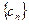 的前项和
的前项和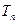 .
.
已知数列{an}中,a1=2,n∈N*,an>0,数列{an}的前n项和为Sn,且满足an+1= .
.
(1)求{Sn}的通项公式;
(2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列.
①求b3;
②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.
设数列{an}的前n项和为Sn.已知a1=1,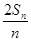 =an+1-
=an+1-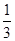 n2-n-
n2-n- ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 .
.
已知数列an=n-16,bn=(-1)n|n-15|,其中n∈N*.
(1)求满足an+1=|bn|的所有正整数n的集合;
(2)若n≠16,求数列 的最大值和最小值;
的最大值和最小值;
(3)记数列{anbn}的前n项和为Sn,求所有满足S2m=S2n(m<n)的有序整数对(m,n).
设无穷数列{an}满足:n∈Ν,an<an+1,an∈N.记bn=aan,cn=aan+1(n∈N*).
(1)若bn=3n(n∈N*),求证:a1=2,并求c1的值;
(2)若{cn}是公差为1的等差数列,问{an}是否为等差数列,证明你的结论.
甲、乙两大超市同时开业,第一年的全年销售额均为a万元,由于经营方式不同,甲超市前n年的总销售额为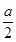 (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多 a万元.
a万元.
(1)设甲、乙两超市第n年的销售额分别为an、bn,求an、bn的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?