(本小题12分)已知函数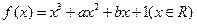 ,函数
,函数 的图像在点
的图像在点 的切线方程是
的切线方程是 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若函数 在区间
在区间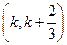 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围.
四棱锥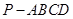 底面是平行四边形,面
底面是平行四边形,面 面
面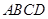 ,
, ,
, ,
, 分别为
分别为 的中点.
的中点.
(1)求证: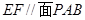 ;
;
(2)求二面角 的余弦值.
的余弦值.
若盒中装有同一型号的灯泡共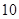 只,其中有
只,其中有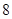 只合格品,
只合格品,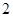 只次品。
只次品。
(1) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求
次,每次取一只灯泡,求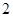 次取到次品的概率;
次取到次品的概率;
(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望.
的分布列和数学期望.
已知函数 .
.
(1)求函数 的最小正周期和最值;
的最小正周期和最值;
(2)求函数 的单调递减区间.
的单调递减区间.
设函数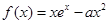 .
.
(1)若 时,求
时,求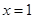 处的切线方程;
处的切线方程;
(2)当 时,
时,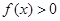 ,求
,求 的取值范围.
的取值范围.
已知 ,其中
,其中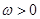 ,若函数
,若函数 ,且函数
,且函数 的图象与直线
的图象与直线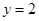 相邻两公共点间的距离为
相邻两公共点间的距离为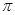 .
.
(1)求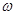 的值;
的值;
(2)在 中.
中.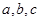 分别是
分别是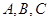 的对边,且
的对边,且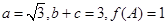 ,求
,求 的面积.
的面积.