21. (本小题满分13分)
设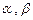 是函数
是函数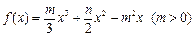 的两个极值点,且
的两个极值点,且 .
.
(1)求证: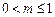 ;
;
(2)求 的取值范围;
的取值范围;
(3)若函数 ,当
,当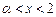 且
且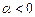 时,求证:
时,求证: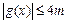 .
.
(本小题满分14分)
已知函数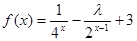 (
(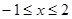 ).
).
(1)若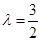 时,求函数
时,求函数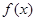 的值域;
的值域;
(2)若函数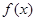 的最小值是1,求实数
的最小值是1,求实数 的值.
的值.
(本小题满分14分)
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台.现销售给A地10台,B地8台.已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.
(本小题满分14分)
已知函数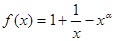 (
( ),且
),且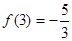 .
.
(1)求α的值;
(2)求函数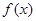 的零点;
的零点;
(3)判断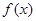 在(-∞,0)上的单调性,并给予证明.
在(-∞,0)上的单调性,并给予证明.
(本小题满分14分)
某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
| 车间 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品自相同车间的概率.
(本小题满分12分)
已知函数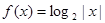 .
.
(1)求函数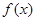 的定义域及
的定义域及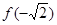 的值;
的值;
(2)判断函数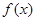 的奇偶性;
的奇偶性;
(3)判断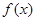 在(0,+∞)上的单调性,并给予证明.
在(0,+∞)上的单调性,并给予证明.